
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 758 Атанасян — Подробные Ответы
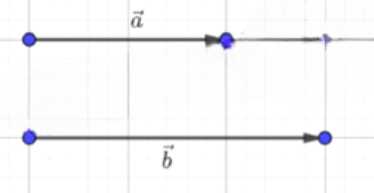
Начертите два ненулевых коллинеарных вектора \( \vec{a} \) и \( \vec{b} \) так, чтобы \( |\vec{a}| \neq |\vec{b}| \). Постройте векторы:
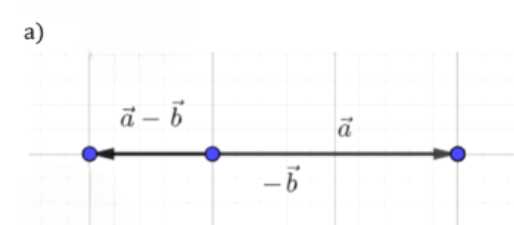
а) \( \vec{a} — \vec{b} \);
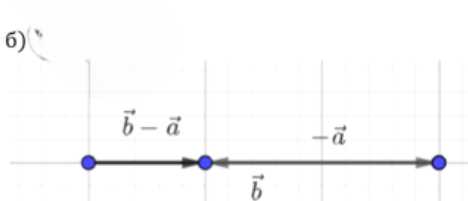
б) \( \vec{b} — \vec{a} \);
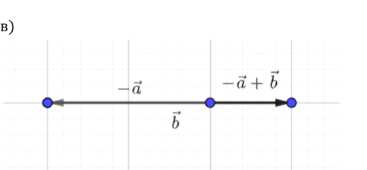
в) \( -\vec{a} + \vec{b} \).
Выполните ещё раз построение для случая, когда \( |\vec{a}| = |\vec{b}| \).
Дано два ненулевых коллинеарных вектора \( \vec{a} \) и \( \vec{b} \), причём \( |\vec{a}| \neq |\vec{b}| \).
Требуется построить векторы:
а) \( \vec{a} — \vec{b} \):
Для вычитания \( \vec{a} — \vec{b} \) необходимо сложить \( \vec{a} \) и \( -\vec{b} \) (вектор \( -\vec{b} \) направлен в противоположную сторону относительно \( \vec{b} \)). Результирующий вектор соединяет начало \( \vec{a} \) с концом \( -\vec{b} \), построенного от конца \( \vec{a} \).
б) \( \vec{b} — \vec{a} \):
Для вычитания \( \vec{b} — \vec{a} \) необходимо сложить \( \vec{b} \) и \( -\vec{a} \) (вектор \( -\vec{a} \) направлен в противоположную сторону относительно \( \vec{a} \)). Результирующий вектор соединяет начало \( \vec{b} \) с концом \( -\vec{a} \), построенного от конца \( \vec{b} \).
в) \( -\vec{a} + \vec{b} \):
Для сложения \( -\vec{a} + \vec{b} \) строится \( -\vec{a} \) (вектор противоположного направления к \( \vec{a} \)) и затем \( \vec{b} \) от конца \( -\vec{a} \). Результирующий вектор соединяет начало \( -\vec{a} \) с концом \( \vec{b} \).
Если \( |\vec{a}| = |\vec{b}| \), то в каждом случае результирующий вектор равен нулевому вектору \( \vec{0} \), поскольку длины векторов равны, а направления противоположны.
Для решения задачи, рассмотрим каждый из случаев отдельно, с подробным объяснением всех этапов построения.
а) Построение вектора \( \vec{a} — \vec{b} \).
Для нахождения разности векторов \( \vec{a} — \vec{b} \) применяется правило, согласно которому вычитание векторов эквивалентно сложению первого вектора с противоположным второму вектору. То есть:
\[ \vec{a} — \vec{b} = \vec{a} + (-\vec{b}) \].
Шаги построения:
1. Построим вектор \( \vec{a} \), который направлен вправо.
2. Построим вектор \( -\vec{b} \), который равен \( \vec{b} \) по длине, но направлен в противоположную сторону (влево).
3. От конца вектора \( \vec{a} \) начертим вектор \( -\vec{b} \).
4. Результирующий вектор \( \vec{a} — \vec{b} \) соединяет начало \( \vec{a} \) с концом \( -\vec{b} \).
б) Построение вектора \( \vec{b} — \vec{a} \).
Аналогично предыдущему случаю, вычитание \( \vec{b} — \vec{a} \) эквивалентно сложению второго вектора с противоположным первому:
\[ \vec{b} — \vec{a} = \vec{b} + (-\vec{a}) \].
Шаги построения:
1. Построим вектор \( \vec{b} \), который направлен влево.
2. Построим вектор \( -\vec{a} \), который равен \( \vec{a} \) по длине, но направлен в противоположную сторону (влево).
3. От конца вектора \( \vec{b} \) начертим вектор \( -\vec{a} \).
4. Результирующий вектор \( \vec{b} — \vec{a} \) соединяет начало \( \vec{b} \) с концом \( -\vec{a} \).
в) Построение вектора \( -\vec{a} + \vec{b} \).
Сложение векторов \( -\vec{a} + \vec{b} \) выполняется по правилу треугольника.
Шаги построения:
1. Построим вектор \( -\vec{a} \), который равен \( \vec{a} \) по длине, но направлен в противоположную сторону (влево).
2. Построим вектор \( \vec{b} \), который направлен влево.
3. От конца вектора \( -\vec{a} \) начертим вектор \( \vec{b} \).
4. Результирующий вектор \( -\vec{a} + \vec{b} \) соединяет начало \( -\vec{a} \) с концом \( \vec{b} \).
Особый случай: если \( |\vec{a}| = |\vec{b}| \).
Если длины векторов \( \vec{a} \) и \( \vec{b} \) равны, то в результате построения в каждом из случаев получится нулевой вектор \( \vec{0} \), так как противоположные направления векторов и равные длины приводят к их взаимной компенсации.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!