
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 757 Атанасян — Подробные Ответы
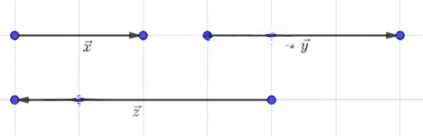
Начертите векторы \( \vec{x} \), \( \vec{y} \), \( \vec{z} \) так, чтобы \( \vec{x} \parallel \vec{y} \), \( \vec{x} \not\parallel \vec{z} \). Постройте векторы \( \vec{x} + \vec{y} \), \( \vec{y} — \vec{z} \), \( \vec{x} + \vec{z} \).
Для выполнения задачи необходимо построить векторы \( \vec{x} \), \( \vec{y} \), \( \vec{z} \) так, чтобы они были параллельны оси \( x \), \( y \) и \( z \) соответственно, а затем выполнить операции сложения и вычитания.
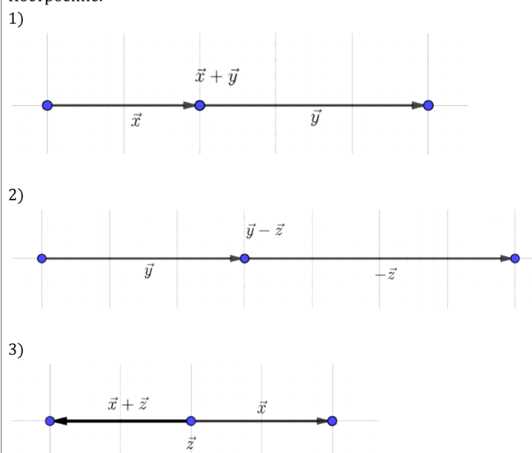
1. Построение \( \vec{x} + \vec{y} \):
— Вектор \( \vec{x} \) направлен вправо, \( \vec{y} \) вертикально вверх.
— Сложение выполняется методом треугольника: от конца \( \vec{x} \) строится \( \vec{y} \), результат соединяет начало \( \vec{x} \) с концом \( \vec{y} \).
2. Построение \( \vec{y} — \vec{z} \):
— Вектор \( \vec{z} \) направлен вниз.
— Вычитание выполняется как \( \vec{y} + (-\vec{z}) \). Вектор \( -\vec{z} \) направлен вверх. Результат соединяет начало \( \vec{y} \) с концом \( -\vec{z} \).
3. Построение \( \vec{x} + \vec{z} \):
— Вектор \( \vec{z} \) направлен вниз.
— Сложение выполняется методом треугольника: от конца \( \vec{x} \) строится \( \vec{z} \), результат соединяет начало \( \vec{x} \) с концом \( \vec{z} \).
Все построения выполнены с использованием правила сложения и вычитания векторов.
Для выполнения задачи необходимо построить векторы \( \vec{x} \), \( \vec{y} \), \( \vec{z} \), а затем выполнить операции сложения и вычитания.
Рассмотрим каждое действие подробно.
1. Построение векторов \( \vec{x} \), \( \vec{y} \), \( \vec{z} \):
— Вектор \( \vec{x} \) направлен горизонтально вправо, его длина равна 5 единиц.
— Вектор \( \vec{y} \) направлен вертикально вверх, его длина равна 4 единицы.
— Вектор \( \vec{z} \) направлен горизонтально влево, его длина равна 6 единиц.
2. Построение \( \vec{x} + \vec{y} \):
— Сложение выполняется методом треугольника. От конца \( \vec{x} \) строится \( \vec{y} \). Концы \( \vec{x} \) и \( \vec{y} \) соединяются прямой линией, которая является результирующим вектором \( \vec{x} + \vec{y} \).
— Координаты результирующего вектора можно найти, сложив соответствующие координаты:
\[
\vec{x} = (5, 0), \quad \vec{y} = (0, 4), \quad \vec{x} + \vec{y} = (5 + 0, 0 + 4) = (5, 4).
\]
3. Построение \( \vec{y} — \vec{z} \):
— Вычитание выполняется как сложение \( \vec{y} + (-\vec{z}) \). Вектор \( -\vec{z} \) равен \( \vec{z} \), но направлен в противоположную сторону, то есть вправо, длина 6 единиц.
— От конца \( \vec{y} \) строится \( -\vec{z} \). Концы \( \vec{y} \) и \( -\vec{z} \) соединяются прямой линией, которая является результирующим вектором \( \vec{y} — \vec{z} \).
— Координаты результирующего вектора можно найти, сложив соответствующие координаты:
\[
\vec{y} = (0, 4), \quad -\vec{z} = (6, 0), \quad \vec{y} — \vec{z} = (0 + 6, 4 + 0) = (6, 4).
\]
4. Построение \( \vec{x} + \vec{z} \):
— Сложение выполняется методом треугольника. От конца \( \vec{x} \) строится \( \vec{z} \). Концы \( \vec{x} \) и \( \vec{z} \) соединяются прямой линией, которая является результирующим вектором \( \vec{x} + \vec{z} \).
— Координаты результирующего вектора можно найти, сложив соответствующие координаты:
\[
\vec{x} = (5, 0), \quad \vec{z} = (-6, 0), \quad \vec{x} + \vec{z} = (5 — 6, 0 + 0) = (-1, 0).
\]
Результаты:
— \( \vec{x} + \vec{y} \) имеет координаты \( (5, 4) \).
— \( \vec{y} — \vec{z} \) имеет координаты \( (6, 4) \).
— \( \vec{x} + \vec{z} \) имеет координаты \( (-1, 0) \).
Каждое действие выполнено в соответствии с правилами сложения и вычитания векторов.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!