ГДЗ по Геометрии 9 класс Номер 756 Атанасян — Подробные Ответы

Начертите попарно неколлинеарные векторы \( \vec{x} \), \( \vec{y} \), \( \vec{z} \) и постройте векторы \( \vec{x} — \vec{y} \), \( \vec{z} — \vec{y} \), \( \vec{x} — \vec{z} \), \( -\vec{x} \), \( -\vec{y} \), \( -\vec{z} \).

Для решения задачи необходимо построить попарно неколлинеарные векторы $\vec{x}$, $\vec{y}$, $\vec{z}$, а также выполнить построение их комбинаций $\vec{x}-\vec{y}$, $\vec{z}-\vec{y}$, $\vec{x}-\vec{z}$, $-\vec{x}$, $-\vec{y}$, $-\vec{z}$.

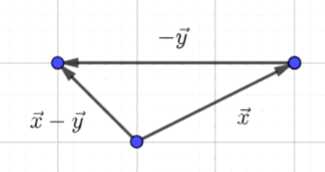
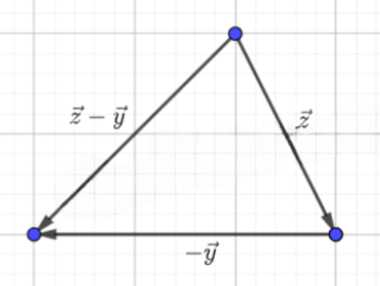
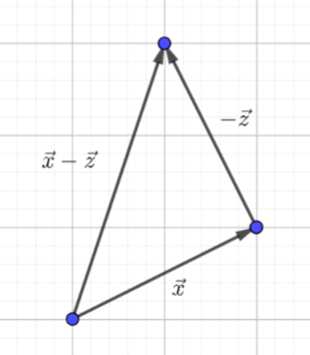
Для решения задачи необходимо построить попарно неколлинеарные векторы \( \vec{x} \), \( \vec{y} \), \( \vec{z} \), а также выполнить построение их комбинаций \( \vec{x} — \vec{y} \), \( \vec{z} — \vec{y} \), \( \vec{x} — \vec{z} \), \( -\vec{x} \), \( -\vec{y} \), \( -\vec{z} \).

1. Построение векторов:
— \( \vec{x} \) направлен вправо, длина 5 единиц.
— \( \vec{y} \) направлен вверх, длина 4 единицы.
— \( \vec{z} \) направлен влево и вверх, длина 6 единиц.

2. Построение разностей векторов:
— \( \vec{x} — \vec{y} \): Строится как \( \vec{x} + (-\vec{y}) \). Вектор \( -\vec{y} \) направлен вниз, длина 4 единицы. Результат соединяет начало \( \vec{x} \) с концом \( -\vec{y} \).
— \( \vec{z} — \vec{y} \): Строится как \( \vec{z} + (-\vec{y}) \). Вектор \( -\vec{y} \) добавляется к \( \vec{z} \), результат соединяет начало \( \vec{z} \) с концом \( -\vec{y} \).
— \( \vec{x} — \vec{z} \): Строится как \( \vec{x} + (-\vec{z}) \). Вектор \( -\vec{z} \) направлен в противоположную сторону от \( \vec{z} \), результат соединяет начало \( \vec{x} \) с концом \( -\vec{z} \).

3. Построение противоположных векторов:
— \( -\vec{x} \): Направлен влево, длина 5 единиц.
— \( -\vec{y} \): Направлен вниз, длина 4 единицы.
— \( -\vec{z} \): Направлен вправо и вниз, длина 6 единиц.

Все построения выполняются строго по правилам сложения и вычитания векторов с использованием координатной системы.