
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 755 Атанасян — Подробные Ответы
Начертите попарно неколлинеарные векторы \( \vec{a} \), \( \vec{b} \), \( \vec{c} \), \( \vec{d} \), \( \vec{e} \) и, пользуясь правилом многоугольника, постройте вектор \( \vec{a} + \vec{b} + \vec{c} + \vec{d} + \vec{e} \).
Для построения суммы векторов \( \vec{a} + \vec{b} + \vec{c} + \vec{d} + \vec{e} \) используем правило многоугольника. Начало каждого следующего вектора совмещается с концом предыдущего, а результирующий вектор соединяет начало первого вектора с концом последнего.
На изображении показано, что:
1. Векторы \( \vec{a}, \vec{b}, \vec{c}, \vec{d}, \vec{e} \) строятся последовательно.
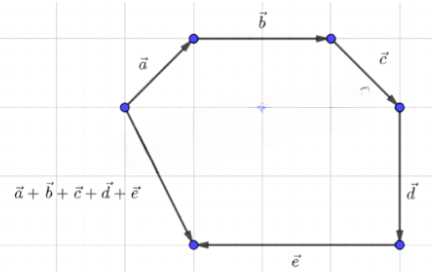
2. Сумма векторов \( \vec{a} + \vec{b} + \vec{c} + \vec{d} + \vec{e} \) представлена диагональю многоугольника, которая соединяет начало первого вектора \( \vec{a} \) с концом последнего вектора \( \vec{e} \).
Ответ: результирующий вектор графически представлен, как показано на рисунке.
Для построения суммы векторов \( \vec{a} + \vec{b} + \vec{c} + \vec{d} + \vec{e} \) используется правило многоугольника, которое заключается в последовательном соединении векторов.
1. Вектор \( \vec{a} \) откладывается от начальной точки. Его направление и длина задаются согласно условию задачи.
2. Вектор \( \vec{b} \) откладывается от конца вектора \( \vec{a} \). Конец вектора \( \vec{b} \) становится новой точкой.
3. Вектор \( \vec{c} \) откладывается от конца вектора \( \vec{b} \). Конец вектора \( \vec{c} \) становится новой точкой.
4. Вектор \( \vec{d} \) откладывается от конца вектора \( \vec{c} \). Конец вектора \( \vec{d} \) становится новой точкой.
5. Вектор \( \vec{e} \) откладывается от конца вектора \( \vec{d} \). Конец вектора \( \vec{e} \) становится новой точкой.
6. Результирующий вектор \( \vec{a} + \vec{b} + \vec{c} + \vec{d} + \vec{e} \) соединяет начало первого вектора \( \vec{a} \) с концом последнего вектора \( \vec{e} \). Это и есть сумма всех данных векторов.
Таким образом, построение выполняется в виде многоугольника, где каждый следующий вектор начинается с конца предыдущего. На изображении показано графическое построение, где результирующий вектор представлен диагональю многоугольника, соединяющей начальную точку с конечной точкой.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!