Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 754 Атанасян — Подробные Ответы
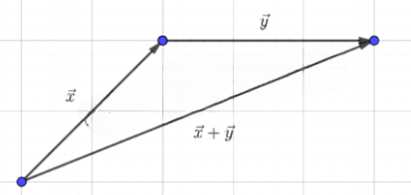
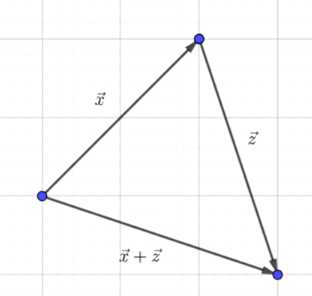
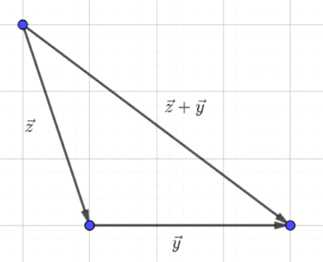
Начертите попарно неколлинеарные векторы \( \vec{x} \), \( \vec{y} \), \( \vec{z} \) и постройте векторы \( \vec{x} + \vec{y} \), \( \vec{x} + \vec{z} \), \( \vec{z} + \vec{y} \).
Для решения задачи выбираем три попарно неколлинеарных вектора \( \vec{x} \), \( \vec{y} \), \( \vec{z} \). Пусть:
\(
\vec{x} = (3, 1), \quad \vec{y} = (1, 4), \quad \vec{z} = (-2, 3).
\)
Сумма двух векторов вычисляется сложением их координат:
\(
\vec{x} + \vec{y} = (3+1, 1+4) = (4, 5),
\)
\(
\vec{x} + \vec{z} = (3+(-2), 1+3) = (1, 4),
\)
\(
\vec{z} + \vec{y} = (-2+1, 3+4) = (-1, 7).
\)
Графически построение выполняется на координатной плоскости, используя правило параллелограмма.
Дано три попарно неколлинеарных вектора \( \vec{x} \), \( \vec{y} \), \( \vec{z} \). Требуется построить их суммы \( \vec{x} + \vec{y} \), \( \vec{x} + \vec{z} \), \( \vec{z} + \vec{y} \).
1. Выбираем координатное представление векторов. Пусть:
\(
\vec{x} = (3, 1), \quad \vec{y} = (1, 4), \quad \vec{z} = (-2, 3).
\)
Координаты векторов указывают на их концы при начале в точке \( (0, 0) \).
2. Для построения суммы векторов используем правило сложения: складываем соответствующие координаты двух векторов.
Считаем суммы:
\(
\vec{x} + \vec{y} = (3+1, 1+4) = (4, 5),
\)
\(
\vec{x} + \vec{z} = (3+(-2), 1+3) = (1, 4),
\)
\(
\vec{z} + \vec{y} = (-2+1, 3+4) = (-1, 7).
\)
3. Построение на плоскости:
Графически векторы строятся следующим образом:
а) Строим векторы \( \vec{x} \), \( \vec{y} \), \( \vec{z} \) из начала координат \( (0, 0) \).
б) Для построения суммы \( \vec{x} + \vec{y} \), переносим начало \( \vec{y} \) в конец \( \vec{x} \) и соединяем начало \( \vec{x} \) с концом \( \vec{y} \).
в) Аналогично строим \( \vec{x} + \vec{z} \) и \( \vec{z} + \vec{y} \).
4. Итоговые координаты сумм:
\(
\vec{x} + \vec{y} = (4, 5), \quad \vec{x} + \vec{z} = (1, 4), \quad \vec{z} + \vec{y} = (-1, 7).
\)
Ответ:
Суммы векторов:
\(
\vec{x} + \vec{y} = (4, 5), \quad \vec{x} + \vec{z} = (1, 4), \quad \vec{z} + \vec{y} = (-1, 7).
\)
Графическое построение выполняется на координатной плоскости с использованием правила параллелограмма.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.