ГДЗ по Геометрии 9 класс Номер 749 Атанасян — Подробные Ответы

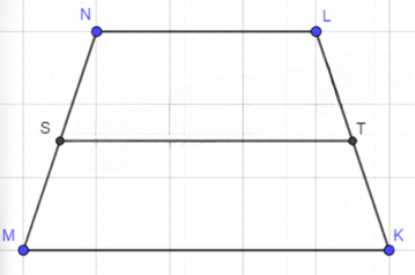
Точки \( S \) и \( T \) являются серединами боковых сторон \( MN \) и \( LK \) равнобедренной трапеции \( MNLK \). Равны ли векторы:  

а) \( \vec{NL} \) и \( \vec{KL} \);  

б) \( \vec{MS} \) и \( \vec{SN} \);  

в) \( \vec{MN} \) и \( \vec{KL} \);  

г) \( \vec{TS} \) и \( \vec{KM} \);  

д) \( \vec{TL} \) и \( \vec{KT} \)?

а) Векторы \( \overrightarrow{NL} \) и \( \overrightarrow{KL} \) не равны, так как они не коллинеарны. Следовательно, \( \overrightarrow{NL} \neq \overrightarrow{KL} \). Ответ: нет.

б) Векторы \( \overrightarrow{MS} \) и \( \overrightarrow{SN} \) равны, так как \(S\) — середина \(MN\), и их длины совпадают: \( | \overrightarrow{MS} | = | \overrightarrow{SN} | \). Следовательно, \( \overrightarrow{MS} = \overrightarrow{SN} \). Ответ: да.

в) Векторы \( \overrightarrow{MN} \) и \( \overrightarrow{KL} \) не равны, так как они не коллинеарны. Следовательно, \( \overrightarrow{MN} \neq \overrightarrow{KL} \). Ответ: нет.

г) Векторы \( \overrightarrow{TS} \) и \( \overrightarrow{KM} \) не равны, так как их длины различны: \( | \overrightarrow{TS} | = \frac{1}{2} | \overrightarrow{KM} | \). Следовательно, \( \overrightarrow{TS} \neq \overrightarrow{KM} \). Ответ: нет.

д) Векторы \( \overrightarrow{TL} \) и \( \overrightarrow{KT} \) равны, так как \(T\) — середина \(KL\), и их длины совпадают: \( | \overrightarrow{TL} | = | \overrightarrow{KT} | \). Следовательно, \( \overrightarrow{TL} = \overrightarrow{KT} \). Ответ: да.

а) Рассмотрим векторы \( \overrightarrow{NL} \) и \( \overrightarrow{KL} \). Точки \(N\), \(L\), \(K\) расположены на разных отрезках равнобедренной трапеции \(ABCD\). Вектор \( \overrightarrow{KL} \) лежит на основании трапеции \(KL\), а вектор \( \overrightarrow{NL} \) соединяет точку \(N\) (середину боковой стороны) с точкой \(L\) (серединой основания). Эти векторы не лежат на одной прямой, их направления различны. Следовательно, \( \overrightarrow{NL} \neq \overrightarrow{KL} \). Ответ: нет.

б) Рассмотрим векторы \( \overrightarrow{MS} \) и \( \overrightarrow{SN} \). Точка \(S\) является серединой отрезка \(MN\), который соединяет середины боковых сторон трапеции. По свойству середины отрезка, длины \(MS\) и \(SN\) равны, а направления векторов совпадают. Таким образом, \( \overrightarrow{MS} = \overrightarrow{SN} \). Ответ: да.

в) Рассмотрим векторы \( \overrightarrow{MN} \) и \( \overrightarrow{KL} \). Вектор \( \overrightarrow{MN} \) соединяет середины боковых сторон трапеции \(ABCD\), а вектор \( \overrightarrow{KL} \) лежит на основании трапеции. Эти векторы не параллельны, так как трапеция равнобедренная, и \(MN\) не является параллельным основанию \(KL\). Следовательно, \( \overrightarrow{MN} \neq \overrightarrow{KL} \). Ответ: нет.

г) Рассмотрим векторы \( \overrightarrow{TS} \) и \( \overrightarrow{KM} \). Точка \(T\) является серединой боковой стороны трапеции, а точка \(S\) — серединой другой боковой стороны. Вектор \( \overrightarrow{TS} \) соединяет середины боковых сторон, и по свойству средней линии трапеции его длина равна половине суммы длин оснований:
\(
| \overrightarrow{TS} | = \frac{1}{2} (|AB| + |CD|).
\)
В то же время, вектор \( \overrightarrow{KM} \) соединяет вершину \(K\) основания с серединой противоположной боковой стороны. Длина \(KM\) не равна длине \(TS\), так как \(KM\) не является средней линией. Следовательно, \( \overrightarrow{TS} \neq \overrightarrow{KM} \). Ответ: нет.

д) Рассмотрим векторы \( \overrightarrow{TL} \) и \( \overrightarrow{KT} \). Точка \(T\) является серединой боковой стороны трапеции, а точка \(L\) — серединой основания \(KL\). По свойству середины, \(T\) делит отрезок \(KL\) пополам, поэтому длины \(TL\) и \(KT\) равны, а направления векторов совпадают. Таким образом, \( \overrightarrow{TL} = \overrightarrow{KT} \). Ответ: да.