ГДЗ по Геометрии 9 класс Номер 748 Атанасян — Подробные Ответы

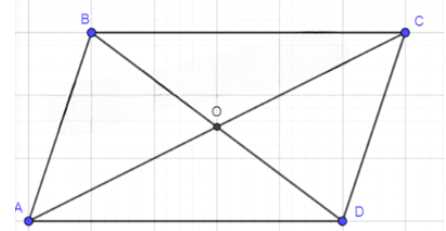
Диагонали параллелограмма \( ABCD \) пересекаются в точке \( O \). Равны ли векторы:  

а) \( \vec{AB} \) и \( \vec{DC} \);  

б) \( \vec{BC} \) и \( \vec{DA} \);  

в) \( \vec{AO} \) и \( \vec{OC} \);  

г) \( \vec{AC} \) и \( \vec{BD} \)?  

Ответ обоснуйте.

а) Векторы \( \overrightarrow{AB} \) и \( \overrightarrow{DC} \) равны, так как противоположные стороны параллелограмма параллельны и равны по длине:
\(
\overrightarrow{AB} \parallel \overrightarrow{DC}, \quad |\overrightarrow{AB}| = |\overrightarrow{DC}|.
\)
Ответ: да.

б) Векторы \( \overrightarrow{BC} \) и \( \overrightarrow{DA} \) не равны, так как это соседние стороны параллелограмма, а не противоположные. Соседние стороны не коллинеарны:
\(
\overrightarrow{BC} \not\parallel \overrightarrow{DA}.
\)
Ответ: нет.

в) Векторы \( \overrightarrow{AO} \) и \( \overrightarrow{OC} \) равны, так как диагонали параллелограмма пересекаются и делятся пополам:
\(
|\overrightarrow{AO}| = |\overrightarrow{OC}|, \quad \overrightarrow{AO} \parallel \overrightarrow{OC}.
\)
Ответ: да.

г) Векторы \( \overrightarrow{AC} \) и \( \overrightarrow{BD} \) не равны, так как диагонали параллелограмма не коллинеарны:
\(
\overrightarrow{AC} \not\parallel \overrightarrow{BD}.
\)
Ответ: нет.

Дано: \( ABCD \) — параллелограмм, \( AC \) и \( BD \) — диагонали, \( AC \cap BD = O \). Необходимо определить, равны ли следующие пары векторов:

а) \( \overrightarrow{AB} \) и \( \overrightarrow{DC} \);
б) \( \overrightarrow{BC} \) и \( \overrightarrow{DA} \);
в) \( \overrightarrow{AO} \) и \( \overrightarrow{OC} \);
г) \( \overrightarrow{AC} \) и \( \overrightarrow{BD} \).

Рассмотрим каждую пару векторов.

а) Векторы \( \overrightarrow{AB} \) и \( \overrightarrow{DC} \) являются противоположными сторонами параллелограмма. По определению параллелограмма, противоположные стороны равны по длине и параллельны. Это означает, что:
\(
\overrightarrow{AB} \parallel \overrightarrow{DC}, \quad |\overrightarrow{AB}| = |\overrightarrow{DC}|.
\)
Следовательно, векторы \( \overrightarrow{AB} \) и \( \overrightarrow{DC} \) равны.
Ответ: да.

б) Векторы \( \overrightarrow{BC} \) и \( \overrightarrow{DA} \) являются соседними сторонами параллелограмма. Соседние стороны параллелограмма не равны по направлению, так как они не коллинеарны. Это видно из того, что угол между \( \overrightarrow{BC} \) и \( \overrightarrow{DA} \) не равен \( 0^\circ \) или \( 180^\circ \). Следовательно,
\(
\overrightarrow{BC} \not\parallel \overrightarrow{DA}.
\)
Ответ: нет.

в) Векторы \( \overrightarrow{AO} \) и \( \overrightarrow{OC} \) соединяют вершины параллелограмма с точкой пересечения диагоналей \( O \). В параллелограмме диагонали пересекаются и делятся пополам. Это означает, что длины отрезков \( AO \) и \( OC \) равны, а направления совпадают:
\(
|\overrightarrow{AO}| = |\overrightarrow{OC}|, \quad \overrightarrow{AO} \parallel \overrightarrow{OC}.
\)
Следовательно, \( \overrightarrow{AO} = \overrightarrow{OC} \).
Ответ: да.

г) Векторы \( \overrightarrow{AC} \) и \( \overrightarrow{BD} \) являются диагоналями параллелограмма. Диагонали пересекаются в точке \( O \), но не лежат на одной прямой. Это означает, что они не коллинеарны. Следовательно,
\(
\overrightarrow{AC} \not\parallel \overrightarrow{BD}.
\)
Ответ: нет.

Итоговые ответы:
а) да;
б) нет;
в) да;
г) нет.