
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 747 Атанасян — Подробные Ответы
Выпишите пары коллинеарных векторов, которые определяются сторонами:
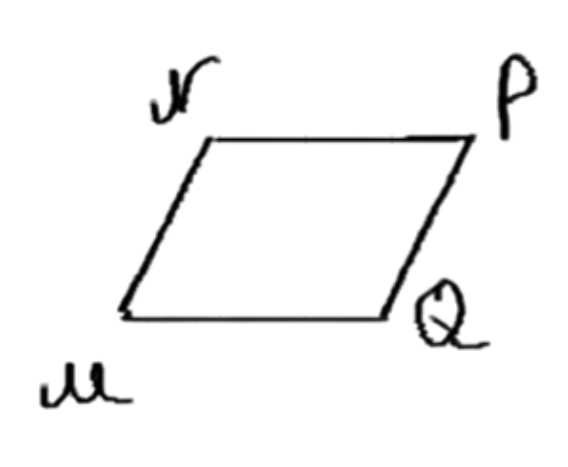
а) параллелограмма \( MNPQ \);
б) трапеции \( ABCD \) с основаниями \( AD \) и \( BC \);
в) треугольника \( FGH \).
Укажите среди них пары сонаправленных и противоположно направленных векторов.
а) Параллелограмм \( MNPQ \):
Коллинеарные:
\(
\overrightarrow{NP} \, \text{и} \, \overrightarrow{MQ}; \quad \overrightarrow{MN} \, \text{и} \, \overrightarrow{PQ}; \quad \overrightarrow{PN} \, \text{и} \, \overrightarrow{QM}; \quad \overrightarrow{MN} \, \text{и} \, \overrightarrow{QP}; \quad \overrightarrow{NP} \, \text{и} \, \overrightarrow{QM}; \)
\(\quad \overrightarrow{PN} \, \text{и} \, \overrightarrow{MQ}; \quad \overrightarrow{NM} \, \text{и} \, \overrightarrow{PQ}; \quad \overrightarrow{NM} \, \text{и} \, \overrightarrow{QP}.
\)
Сонаправленные:
\(
\overrightarrow{NP} \, \text{и} \, \overrightarrow{MQ}; \quad \overrightarrow{PN} \, \text{и} \, \overrightarrow{QM}; \quad \overrightarrow{NM} \, \text{и} \, \overrightarrow{PQ}; \quad \overrightarrow{MN} \, \text{и} \, \overrightarrow{QP}.
\)
Противоположно направленные:
\(
\overrightarrow{NP} \, \text{и} \, \overrightarrow{QM}; \quad \overrightarrow{PN} \, \text{и} \, \overrightarrow{MQ}; \quad \overrightarrow{NM} \, \text{и} \, \overrightarrow{QP}; \quad \overrightarrow{MN} \, \text{и} \, \overrightarrow{PQ}.
\)
б) Трапеция \( ABCD \) с основаниями \( AD \) и \( BC \):
Коллинеарные:
\(
\overrightarrow{BC} \, \text{и} \, \overrightarrow{AD}; \quad \overrightarrow{BC} \, \text{и} \, \overrightarrow{DA}; \quad \overrightarrow{CB} \, \text{и} \, \overrightarrow{DA}; \quad \overrightarrow{CB} \, \text{и} \, \overrightarrow{AD}.
\)
Сонаправленные:
\(
\overrightarrow{BC} \, \text{и} \, \overrightarrow{AD}; \quad \overrightarrow{CE} \, \text{и} \, \overrightarrow{DA}.
\)
Противоположно направленные:
\(
\overrightarrow{BC} \, \text{и} \, \overrightarrow{DA}; \quad \overrightarrow{CB} \, \text{и} \, \overrightarrow{AD}.
\)
в) Треугольник \( FGH \):
Для треугольника \( FGH \) нужно указать пары коллинеарных, сонаправленных и противоположно направленных векторов, но данные в задаче отсутствуют. Если требуется, уточните условия.
а) Параллелограмм \( MNPQ \):
Коллинеарные:
\(
\overrightarrow{NP} \, \text{и} \, \overrightarrow{MQ}; \quad \overrightarrow{MN} \, \text{и} \, \overrightarrow{PQ}; \quad \overrightarrow{PN} \, \text{и} \, \overrightarrow{QM}; \quad \overrightarrow{MN} \, \text{и} \, \overrightarrow{QP}; \quad \overrightarrow{NP} \, \text{и} \, \overrightarrow{QM}; \quad \)
\(\overrightarrow{PN} \, \text{и} \, \overrightarrow{MQ}; \quad \overrightarrow{NM} \, \text{и} \, \overrightarrow{PQ}; \quad \overrightarrow{NM} \, \text{и} \, \overrightarrow{QP}.
\)
Сонаправленные:
\(
\overrightarrow{NP} \, \text{и} \, \overrightarrow{MQ}; \quad \overrightarrow{PN} \, \text{и} \, \overrightarrow{QM}; \quad \overrightarrow{NM} \, \text{и} \, \overrightarrow{PQ}; \quad \overrightarrow{MN} \, \text{и} \, \overrightarrow{QP}.
\)
Противоположно направленные:
\(
\overrightarrow{NP} \, \text{и} \, \overrightarrow{QM}; \quad \overrightarrow{PN} \, \text{и} \, \overrightarrow{MQ}; \quad \overrightarrow{NM} \, \text{и} \, \overrightarrow{QP}; \quad \overrightarrow{MN} \, \text{и} \, \overrightarrow{PQ}.
\)
б) Трапеция \( ABCD \) с основаниями \( AD \) и \( BC \):
Коллинеарные:
\(
\overrightarrow{BC} \, \text{и} \, \overrightarrow{AD}; \quad \overrightarrow{BC} \, \text{и} \, \overrightarrow{DA}; \quad \overrightarrow{CB} \, \text{и} \, \overrightarrow{DA}; \quad \overrightarrow{CB} \, \text{и} \, \overrightarrow{AD}.
\)
Сонаправленные:
\(
\overrightarrow{BC} \, \text{и} \, \overrightarrow{AD}; \quad \overrightarrow{CE} \, \text{и} \, \overrightarrow{DA}.
\)
Противоположно направленные:
\(
\overrightarrow{BC} \, \text{и} \, \overrightarrow{DA}; \quad \overrightarrow{CB} \, \text{и} \, \overrightarrow{AD}.
\)
в) Треугольник \( FGH \):
Для треугольника \( FGH \) нужно указать пары коллинеарных, сонаправленных и противоположно направленных векторов, но данные в задаче отсутствуют. Если требуется, уточните условия.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!