
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 745 Атанасян — Подробные Ответы
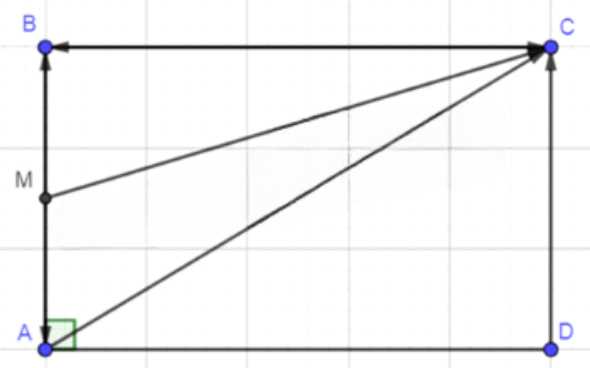
В прямоугольнике \( ABCD \) \( AB = 3 \, \text{см} \), \( BC = 4 \, \text{см} \), \( M \) — середина стороны \( AB \). Найдите длины векторов \( \vec{AB} \), \( \vec{BC} \), \( \vec{DC} \), \( \vec{MC} \), \( \vec{MA} \), \( \vec{CB} \), \( \vec{AC} \).
Дано: ABCD — прямоугольник, AB = 3 см, BC = 4 см, CD = 3 см, M — середина AB.
Найти: |AB|, |BC|, |DC|, |MC|, |MA|, |CB|, |AC|.
Решение:
1) |AB| = 3 см
2) |BC| = |CB| = 4 см
3) |DC| = 3 см (так как AB = CD по определению прямоугольника)
4) |MA| = \( \frac{1}{2} \cdot |AB| = \frac{3}{2} = 1,5 \, \text{см} \)
5) По теореме Пифагора:
\(
MC = \sqrt{CB^2 + BM^2} = \sqrt{16 + 2,25} = \sqrt{18,25} \approx 4,27 \, \text{см}.
\)
6) |AC| = \( \sqrt{BC^2 + AB^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \, \text{см} \).
Ответ:
|AB| = 3 см, |BC| = 4 см, |DC| = 3 см, |MC| ≈ 4,27 см, |MA| = 1,5 см, |CB| = 4 см, |AC| = 5 см.
Дано: ABCD — прямоугольник, AB = 3 см, BC = 4 см, CD = 3 см, M — середина AB.
Найти: |AB|, |BC|, |DC|, |MC|, |MA|, |CB|, |AC|.
Решение:
1) По условию задачи |AB| = 3 см.
2) По условию задачи |BC| = 4 см, а так как стороны прямоугольника, противоположные друг другу, равны, то |CB| = |BC| = 4 см.
3) По свойствам прямоугольника |DC| = |AB|, следовательно, |DC| = 3 см.
4) Найдем длину отрезка |MA|. Так как M — середина отрезка AB, то |MA| равна половине длины |AB|:
\(
|MA| = \frac{|AB|}{2} = \frac{3}{2} = 1,5 \, \text{см}.
\)
5) Найдем длину отрезка |MC|. Для этого используем теорему Пифагора в прямоугольном треугольнике MCB, где |MC| — гипотенуза, |CB| = 4 см, а |BM| = |MA| = 1,5 см.
По теореме Пифагора:
\(
|MC| = \sqrt{|CB|^2 + |BM|^2}.
\)
Подставляем значения:
\(
|MC| = \sqrt{4^2 + 1,5^2} = \sqrt{16 + 2,25} = \sqrt{18,25}.
\)
В десятичной форме:
\(
|MC| \approx 4,27 \, \text{см}.
\)
6) Найдем длину отрезка |AC|. Для этого используем теорему Пифагора в прямоугольном треугольнике ABC, где |AC| — гипотенуза, |AB| = 3 см, |BC| = 4 см.
По теореме Пифагора:
\(
|AC| = \sqrt{|AB|^2 + |BC|^2}.
\)
Подставляем значения:
\(
|AC| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \, \text{см}.
\)
Ответ:
|AB| = 3 см, |BC| = 4 см, |DC| = 3 см, |MC| ≈ 4,27 см, |MA| = 1,5 см, |CB| = 4 см, |AC| = 5 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!