Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 743 Атанасян — Подробные Ответы
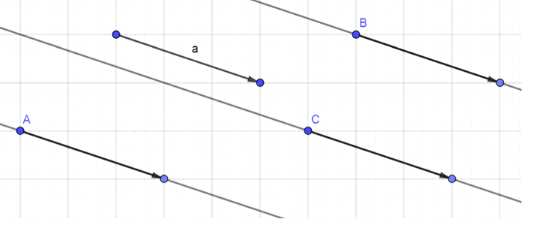
Начертите ненулевой вектор \( \vec{a} \) и отметьте на плоскости три точки \( A \), \( B \) и \( C \). Отложите от точек \( A \), \( B \) и \( C \) векторы, равные \( \vec{a} \).
Дано: точки \( A, B, C \) и вектор \( \vec{a} \).
Решение:
1. Через точки \( A, B, C \) проведем прямые, параллельные направлению вектора \( \vec{a} \).
2. На каждой из этих прямых отложим отрезки, равные длине \( |\vec{a}| \), сохраняя направление вектора \( \vec{a} \).
Результат: от каждой из точек \( A, B, C \) отложены векторы, равные \( \vec{a} \).
Дано: точки \( A, B, C \) и вектор \( \vec{a} \). Требуется отложить от точек \( A, B, C \) векторы, равные вектору \( \vec{a} \).
Решение:
1. Определим направление и длину вектора \( \vec{a} \). Вектор \( \vec{a} \) задается направлением и длиной \( |\vec{a}| \).
2. Через каждую из точек \( A, B, C \) проведем прямую, параллельную направлению вектора \( \vec{a} \). Это можно сделать с помощью линейки и угольника или графического построения.
3. На каждой из построенных прямых отложим отрезок, равный длине \( |\vec{a}| \), начиная от точки \( A, B, C \). Отрезки должны быть направлены в ту же сторону, что и \( \vec{a} \).
4. Полученные отрезки на прямых будут представлять собой векторы \( \vec{a_1}, \vec{a_2}, \vec{a_3} \), равные вектору \( \vec{a} \).
Результат: от каждой из точек \( A, B, C \) отложены векторы \( \vec{a_1}, \vec{a_2}, \vec{a_3} \), равные вектору \( \vec{a} \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.