Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 742 Атанасян — Подробные Ответы
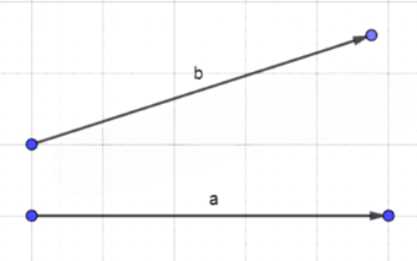
Начертите два вектора:
а) имеющие равные длины и неколлинеарные;
б) имеющие равные длины и сонаправленные;
в) имеющие равные длины и противоположно направленные.
В каком случае полученные векторы равны?
Для выполнения задания:
а) Построим два вектора \( \vec{a} \) и \( \vec{b} \), имеющие равные длины, но неколлинеарные. Например, \( \vec{a} \) направим вправо, а \( \vec{b} \) — вверх. Такие векторы не лежат на одной прямой и имеют одинаковую длину.
б) Построим два вектора \( \vec{c} \) и \( \vec{d} \), имеющие равные длины и сонаправленные. Например, оба вектора направлены вправо, и их длины равны. В этом случае векторы коллинеарны и направлены одинаково.
в) Построим два вектора \( \vec{e} \) и \( \vec{f} \), имеющие равные длины, но противоположно направленные. Например, \( \vec{e} \) направлен вправо, а \( \vec{f} \) — влево. Такие векторы коллинеарны, но их направления противоположны.
Полученные векторы равны в случае, если они имеют одинаковую длину, одинаковое направление и лежат на одной прямой (случай б).
Для выполнения задания с подробным решением:
а) Построим два вектора \( \vec{a} \) и \( \vec{b} \), имеющие равные длины и неколлинеарные.
Необходимо, чтобы длины векторов были равны, но направления отличались. Например:
— Вектор \( \vec{a} \) имеет длину \( |\vec{a}| = 5 \) и направлен горизонтально вправо.
— Вектор \( \vec{b} \) имеет длину \( |\vec{b}| = 5 \) и направлен вертикально вверх.
Эти векторы не лежат на одной прямой, так как их направления различны (один горизонтальный, другой вертикальный). Они неколлинеарны, но их длины равны.
б) Построим два вектора \( \vec{c} \) и \( \vec{d} \), имеющие равные длины и сонаправленные.
Необходимо, чтобы длины были равны, и направления совпадали. Например:
— Вектор \( \vec{c} \) имеет длину \( |\vec{c}| = 4 \) и направлен вправо.
— Вектор \( \vec{d} \) также имеет длину \( |\vec{d}| = 4 \) и направлен вправо.
Эти векторы лежат на одной прямой, их направления совпадают, и длины равны. В этом случае векторы коллинеарны и сонаправлены.
в) Построим два вектора \( \vec{e} \) и \( \vec{f} \), имеющие равные длины и противоположно направленные.
Необходимо, чтобы длины были равны, но направления противоположны. Например:
— Вектор \( \vec{e} \) имеет длину \( |\vec{e}| = 3 \) и направлен вправо.
— Вектор \( \vec{f} \) имеет длину \( |\vec{f}| = 3 \), но направлен влево.
Эти векторы лежат на одной прямой, их направления противоположны, но длины равны. В этом случае векторы коллинеарны и противоположно направлены.
Векторы равны в случае, если их длины равны, они лежат на одной прямой и их направления совпадают. Это выполняется в случае б), где \( \vec{c} = \vec{d} \).
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.