
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 741 Атанасян — Подробные Ответы
Начертите два неколлинеарных вектора \( \vec{a} \) и \( \vec{b} \). Изобразите несколько векторов:
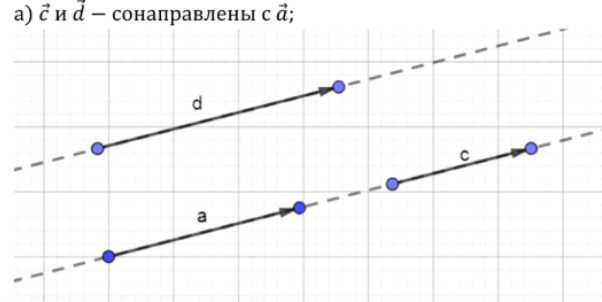
а) сонаправленных с вектором \( \vec{a} \);
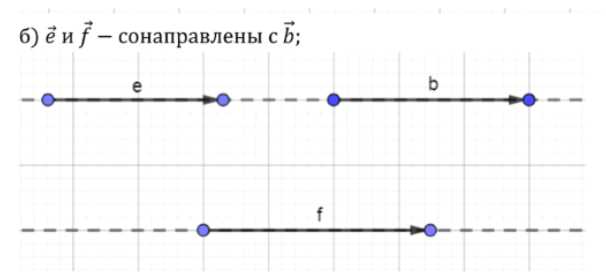
б) сонаправленных с вектором \( \vec{b} \);
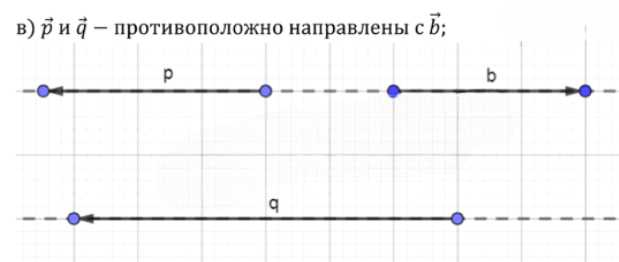
в) противоположно направленных вектору \( \vec{b} \);
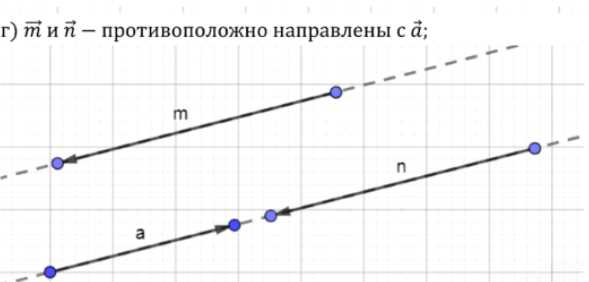
г) противоположно направленных вектору \( \vec{a} \).
Для выполнения задания:
1. Начертите два неколлинеарных вектора \( \vec{a} \) и \( \vec{b} \), которые не лежат на одной прямой. Например, вектор \( \vec{a} \) направлен вправо, а вектор \( \vec{b} \) направлен вверх.
2. Сонаправленные с вектором \( \vec{a} \):
Постройте несколько векторов, которые имеют то же направление, что и \( \vec{a} \). Эти векторы должны быть параллельны \( \vec{a} \), например, увеличенные или уменьшенные в длине, но направленные вправо.
3. Сонаправленные с вектором \( \vec{b} \):
Постройте несколько векторов, которые имеют то же направление, что и \( \vec{b} \). Эти векторы должны быть параллельны \( \vec{b} \), например, увеличенные или уменьшенные в длине, но направленные вверх.
4. Противоположно направленные вектору \( \vec{b} \):
Постройте несколько векторов, которые направлены в противоположную сторону относительно \( \vec{b} \). Эти векторы должны быть параллельны \( \vec{b} \), но направлены вниз.
5. Противоположно направленные вектору \( \vec{a} \):
Постройте несколько векторов, которые направлены в противоположную сторону относительно \( \vec{a} \). Эти векторы должны быть параллельны \( \vec{a} \), но направлены влево.
Итог: все векторы должны быть правильно расположены относительно \( \vec{a} \) и \( \vec{b} \), соблюдая их направления.
Для выполнения задания с построением векторов:
1. Начертим два неколлинеарных вектора \( \vec{a} \) и \( \vec{b} \). Это означает, что \( \vec{a} \) и \( \vec{b} \) не лежат на одной прямой. Например:
— Вектор \( \vec{a} \) направим вправо (горизонтально).
— Вектор \( \vec{b} \) направим вверх (вертикально).
2. Построим несколько векторов, сонаправленных с вектором \( \vec{a} \).
Сонаправленные векторы имеют то же направление, что и \( \vec{a} \), но могут отличаться по длине. Например:
— Построим вектор \( \vec{c} \), равный \( 2 \cdot \vec{a} \), то есть в два раза длиннее \( \vec{a} \), но направленный вправо.
— Построим вектор \( \vec{d} \), равный \( 0.5 \cdot \vec{a} \), то есть в два раза короче \( \vec{a} \), но также направленный вправо.
3. Построим несколько векторов, сонаправленных с вектором \( \vec{b} \).
Сонаправленные векторы имеют то же направление, что и \( \vec{b} \), но могут отличаться по длине. Например:
— Построим вектор \( \vec{e} \), равный \( 3 \cdot \vec{b} \), то есть в три раза длиннее \( \vec{b} \), но направленный вверх.
— Построим вектор \( \vec{f} \), равный \( 0.25 \cdot \vec{b} \), то есть в четыре раза короче \( \vec{b} \), но также направленный вверх.
4. Построим несколько векторов, противоположно направленных вектору \( \vec{b} \).
Противоположно направленные векторы имеют направление, обратное \( \vec{b} \), то есть вниз. Например:
— Построим вектор \( \vec{g} \), равный \( -\vec{b} \), то есть равный по длине \( \vec{b} \), но направленный вниз.
— Построим вектор \( \vec{h} \), равный \( -2 \cdot \vec{b} \), то есть в два раза длиннее \( \vec{b} \), но направленный вниз.
5. Построим несколько векторов, противоположно направленных вектору \( \vec{a} \).
Противоположно направленные векторы имеют направление, обратное \( \vec{a} \), то есть влево. Например:
— Построим вектор \( \vec{i} \), равный \( -\vec{a} \), то есть равный по длине \( \vec{a} \), но направленный влево.
— Построим вектор \( \vec{j} \), равный \( -0.5 \cdot \vec{a} \), то есть в два раза короче \( \vec{a} \), но направленный влево.
Итоговое построение должно включать:
а) несколько векторов, сонаправленных с \( \vec{a} \), направленных вправо;
б) несколько векторов, сонаправленных с \( \vec{b} \), направленных вверх;
в) несколько векторов, противоположно направленных \( \vec{b} \), направленных вниз;
г) несколько векторов, противоположно направленных \( \vec{a} \), направленных влево.
Каждый вектор строится с учетом направления и длины.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!