ГДЗ по Геометрии 9 класс Номер 740 Атанасян — Подробные Ответы

Начертите векторы \( \vec{AB} \), \( \vec{CD} \) и \( \vec{EF} \) так, чтобы:  

а) \( \vec{AB} \), \( \vec{CD} \) и \( \vec{EF} \) были коллинеарны и \( |\vec{AB}| = 1 \, \text{см} \), \( |\vec{CD}| = 2,5 \, \text{см} \), \( |\vec{EF}| = 4,5 \, \text{см} \);  

б) \( \vec{AB} \) и \( \vec{EF} \) были коллинеарны, \( \vec{AB} \) и \( \vec{CD} \) были не коллинеарны и \( |\vec{AB}| = 3 \, \text{см} \), \( |\vec{CD}| = 1,5 \, \text{см} \), \( |\vec{EF}| = 1 \, \text{см} \).

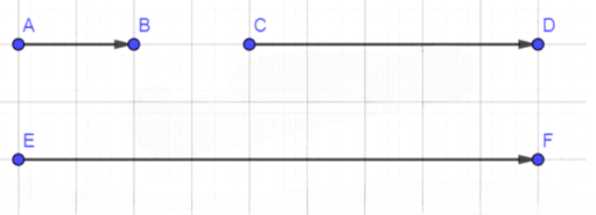
а) Так как \( \overrightarrow{AB}, \overrightarrow{CD} \) и \( \overrightarrow{EF} \) коллинеарны, их направления совпадают, и они расположены на одной прямой. Длины отрезков указаны:
\[ |AB| = 1 \, \text{см}, \quad |CD| = 2 \frac{1}{2} \, \text{см}, \quad |EF| = 4 \frac{1}{2} \, \text{см}. \]
Решение заключается в том, чтобы построить отрезки на одной прямой, соблюдая указанные длины.

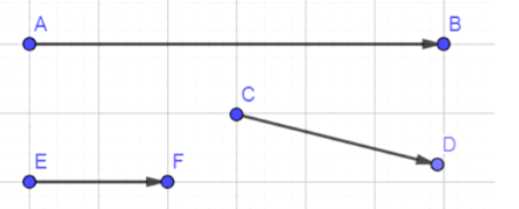
б) \( \overrightarrow{AB} \) и \( \overrightarrow{EF} \) коллинеарны, то есть лежат на одной прямой, а \( \overrightarrow{AB} \) и \( \overrightarrow{CD} \) не коллинеарны, то есть направления этих векторов различны. Построить:
1. Отрезок \( AB \) длиной \( 1 \, \text{см} \).
2. Отрезок \( CD \) длиной \( 2 \frac{1}{2} \, \text{см} \), направленный под углом к \( AB \).
3. Отрезок \( EF \) длиной \( 4 \frac{1}{2} \, \text{см} \), коллинеарный \( AB \).

а) Рассмотрим случай, когда \( \overrightarrow{AB}, \overrightarrow{CD} \) и \( \overrightarrow{EF} \) коллинеарны. Это означает, что все три отрезка лежат на одной прямой, и их направления совпадают.

Для построения:

1. Отрезок \( AB \) имеет длину \( |AB| = 1 \, \text{см} \).
Его можно изобразить на прямой, начав с точки \( A \) и отложив вправо \( 1 \, \text{см} \) до точки \( B \).

2. Отрезок \( CD \) имеет длину \( |CD| = 2 \frac{1}{2} \, \text{см} \).
Следующий отрезок \( CD \) также лежит на той же прямой и начинается от точки \( C \), расположенной на продолжении \( AB \). Длина отрезка \( CD \) равна \( 2 \frac{1}{2} \, \text{см} \), что можно отложить дальше на прямой.

3. Отрезок \( EF \) имеет длину \( |EF| = 4 \frac{1}{2} \, \text{см} \).
Третий отрезок \( EF \) также лежит на той же прямой. Начальная точка \( E \) должна быть на продолжении \( CD \), а длина отрезка равна \( 4 \frac{1}{2} \, \text{см} \).

Итог: все три отрезка расположены на одной прямой, их длины и последовательность соблюдены. Построение завершено.

б) Рассмотрим случай, когда \( \overrightarrow{AB} \) и \( \overrightarrow{EF} \) коллинеарны, но \( \overrightarrow{AB} \) и \( \overrightarrow{CD} \) не коллинеарны. Это означает, что \( AB \) и \( EF \) лежат на одной прямой, а \( CD \) располагается под углом к ним.

Для построения:

1. Отрезок \( AB \) имеет длину \( |AB| = 1 \, \text{см} \).
Его можно изобразить на прямой, начав с точки \( A \) и отложив вправо \( 1 \, \text{см} \) до точки \( B \).

2. Отрезок \( CD \) имеет длину \( |CD| = 2 \frac{1}{2} \, \text{см} \).
Так как \( AB \) и \( CD \) не коллинеарны, \( CD \) располагается под углом к \( AB \). Начальная точка \( C \) может быть выбрана произвольно, но при этом направление \( CD \) должно быть отличным от направления \( AB \). Длина отрезка равна \( 2 \frac{1}{2} \, \text{см} \).

3. Отрезок \( EF \) имеет длину \( |EF| = 4 \frac{1}{2} \, \text{см} \).
Отрезок \( EF \) коллинеарен \( AB \), то есть лежит на той же прямой, что и \( AB \). Начальная точка \( E \) должна быть на продолжении \( AB \), а длина отрезка равна \( 4 \frac{1}{2} \, \text{см} \).

Итог: \( AB \) и \( EF \) лежат на одной прямой, \( CD \) располагается под углом к ним. Построение завершено.