
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 739 Атанасян — Подробные Ответы
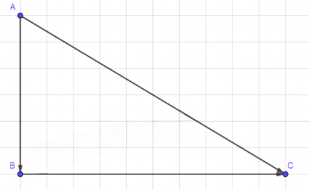
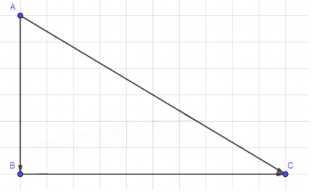
Выбрав подходящий масштаб, начертите векторы, изображающие полёт самолёта сначала на 300 км на юг от города \( A \) до \( B \), а потом на 500 км на восток от города \( B \) до \( C \). Затем начертите вектор \( \vec{AC} \), который изображает перемещение из начальной точки в конечную.
Для решения задачи:
1. Масштаб: \( 1 \, \text{см} = 100 \, \text{км} \), что соответствует \( 1 : 10\,000\,000 \).
2. Построение:
— От точки \( A \) вниз (на юг) откладывается отрезок длиной \( 3 \, \text{см} \), что соответствует 300 км. Получаем точку \( B \).
— От точки \( B \) вправо (на восток) откладывается отрезок длиной \( 5 \, \text{см} \), что соответствует 500 км. Получаем точку \( C \).
— Соединяем точки \( A \) и \( C \), чтобы получить вектор \( \overrightarrow{AC} \).
3. Вектор \( \overrightarrow{AC} \) показывает направление движения самолета из точки \( A \) в точку \( C \).
Для решения задачи необходимо выполнить следующие шаги:
1. Условие задачи: самолет летит сначала на 300 км на юг из точки \( A \) в точку \( B \), затем на 500 км на восток из точки \( B \) в точку \( C \). Требуется построить векторы, изображающие эти перемещения, а также вектор \( \overrightarrow{AC} \), соединяющий начальную и конечную точки. Масштаб: \( 1 \, \text{см} = 100 \, \text{км} \).
2. Перевод расстояний в масштаб:
300 км на юг соответствует \( \frac{300}{100} = 3 \, \text{см} \).
500 км на восток соответствует \( \frac{500}{100} = 5 \, \text{см} \).
3. Построение векторов:
из точки \( A \) вниз (на юг) откладывается отрезок длиной \( 3 \, \text{см} \), что соответствует перемещению из \( A \) в \( B \).
из точки \( B \) вправо (на восток) откладывается отрезок длиной \( 5 \, \text{см} \), что соответствует перемещению из \( B \) в \( C \).
4. Построение вектора \( \overrightarrow{AC} \): соединяем точки \( A \) и \( C \) прямой линией, которая представляет вектор \( \overrightarrow{AC} \).
5. Вычисление длины вектора \( \overrightarrow{AC} \):
по теореме Пифагора длина вектора \( \overrightarrow{AC} \) равна:
\( AC = \sqrt{AB^2 + BC^2} \)
подставляем значения:
\( AC = \sqrt{(300)^2 + (500)^2} = \sqrt{90000 + 250000} = \sqrt{340000} \)
\( AC = \sqrt{340000} = 100\sqrt{34} \approx 583,1 \, \text{км} \)
длина вектора \( AC \) составляет примерно \( 583,1 \, \text{км} \).
6. Определение направления вектора \( \overrightarrow{AC} \):
направление задается углом между вектором и осью \( x \) (восток). Используем формулу тангенса угла:
\( \tan \alpha = \frac{AB}{BC} \)
подставляем значения:
\( \tan \alpha = \frac{300}{500} = 0,6 \)
находим угол:
\( \alpha = \arctan(0,6) \approx 31^\circ \)
вектор \( \overrightarrow{AC} \) наклонен под углом примерно \( 31^\circ \) к оси \( x \) (восток).
Ответ: длина вектора \( \overrightarrow{AC} \) составляет \( 583,1 \, \text{км} \), его направление задается углом \( 31^\circ \) к оси \( x \) (восток). Построение выполнено с использованием масштаба \( 1 \, \text{см} = 100 \, \text{км} \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!