Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 738 Атанасян — Подробные Ответы
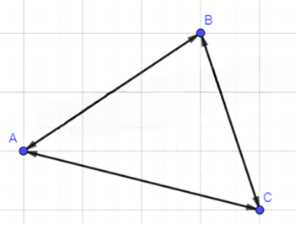
Отметьте точки \( A \), \( B \) и \( C \), не лежащие на одной прямой. Начертите все ненулевые векторы, начало и конец которых совпадают с какими-то двумя из этих точек. Выпишите все полученные векторы и укажите начало и конец каждого вектора.
Для решения задачи отметьте точки \( A \), \( B \), \( C \), которые не лежат на одной прямой.
Постройте все ненулевые векторы, начало и конец которых совпадают с этими точками:
\[
\overrightarrow{AB}, \overrightarrow{BA}, \overrightarrow{AC}, \overrightarrow{CA}, \overrightarrow{BC}, \overrightarrow{CB}.
\]
Для полного решения задачи необходимо выполнить следующие шаги:
1. Отметьте точки \( A \), \( B \), \( C \) на координатной плоскости так, чтобы они не лежали на одной прямой. Это условие исключает возможность коллинеарности точек, то есть они должны образовывать треугольник.
2. Постройте все ненулевые векторы, начало и конец которых совпадают с этими точками. В данном случае точки \( A \), \( B \), \( C \) являются началом и концом векторов. Для каждой пары точек строится два вектора: один направлен от первой точки ко второй, а другой — в обратном направлении.
Перечислим все возможные векторы:
\(
\overrightarrow{AB}: A — \text{начало вектора}; B — \text{конец вектора}.
\)
\(
\overrightarrow{BA}: B — \text{начало вектора}; A — \text{конец вектора}.
\)
\(
\overrightarrow{AC}: A — \text{начало вектора}; C — \text{конец вектора}.
\)
\(
\overrightarrow{CA}: C — \text{начало вектора}; A — \text{конец вектора}.
\)
\(
\overrightarrow{BC}: B — \text{начало вектора}; C — \text{конец вектора}.
\)
\(
\overrightarrow{CB}: C — \text{начало вектора}; B — \text{конец вектора}.
\)
3. Для построения каждого вектора на координатной плоскости необходимо соединить начальную точку с конечной стрелкой, указывающей направление вектора.
4. Убедитесь, что все векторы имеют ненулевую длину. Это условие выполняется автоматически, так как точки \( A \), \( B \), \( C \) не лежат на одной прямой и не совпадают друг с другом.
Таким образом, построены все ненулевые векторы, начало и конец которых совпадают с заданными точками \( A \), \( B \), \( C \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.