
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1104 Атанасян — Подробные Ответы
a) Длина окружности, описанной около правильного треугольника со стороной a
б) Длина окружности, описанной около прямоугольного треугольника с катетами a и b
в) Длина окружности, описанной около равнобедренного треугольника с основанием a и боковой стороной b
г) Длина окружности, описанной около прямоугольника с меньшей стороной a и острым углом α между диагоналями
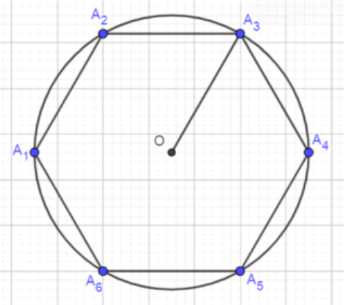
д) Длина окружности, описанной около правильного шестиугольника с площадью S = 24/3 см²
a) Дано: ΔABC — правильный, AB = a
Решение:
\(a_3 = 2R \cdot \sin 60^\circ = 2R \cdot \sqrt{3} \Rightarrow R = \frac{a_3}{\sqrt{3}} = \frac{a}{\sqrt{3}}\)
\(C = 2\pi R = 2\pi \cdot \frac{a}{\sqrt{3}} = \frac{2\sqrt{3}\pi a}{3}\)
б) Дано: ΔABC — прямоугольный, ∠C = 90°, AC = a, CB = b
Решение:
\(AB = d \Rightarrow AB = \sqrt{a^2 + b^2}\)
\(AO = OB = \frac{AB}{2} = \frac{\sqrt{a^2 + b^2}}{2} = R\)
\(C = 2\pi R = 2\pi \cdot \frac{\sqrt{a^2 + b^2}}{2} = \pi\sqrt{a^2 + b^2}\)
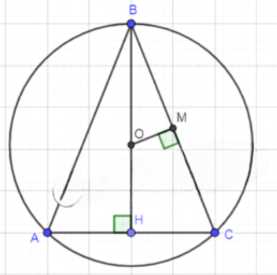
в) Дано: ΔABC — равнобедренный, AC = a, AB = BC = b
Решение:
1) OB = R, BM = MC, OM ⊥ BC
2) Рассмотрим ΔBHC и ΔOEM: ∠HBC — общий, ∠OEB = ∠BHC = 90°, значит ΔBHC ~ ΔOEM (по 2 углам), OB/BC = BM/BM => OB = BH
3) Рассмотрим ΔBHC — прямоугольный:
\(BH = \sqrt{BC^2 — HC^2} = \sqrt{b^2 — \left(\frac{a}{2}\right)^2} = \sqrt{b^2 — \frac{a^2}{4}} = \frac{\sqrt{4b^2 — a^2}}{2}\)
4) OB = \(\frac{b \cdot b \cdot 2}{2\sqrt{4b^2 — a^2}} = \frac{b^2}{\sqrt{4b^2 — a^2}} = R\)
5) C = 2πR = \(\frac{2πb^2}{\sqrt{4b^2 — a^2}}\)
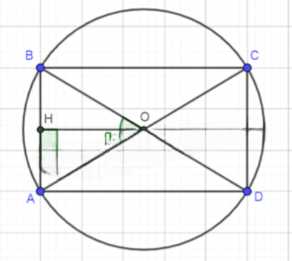
г)
1) AC = BD = d;
2) BO = OC = AO = OD = R (по свойству прямоугольника);
3) Рассмотрим ΔAOB:
OB = OA ⇒ ΔAOB — равнобедренный;
OH — высота, медиана и биссектриса (по свойству);
4) Рассмотрим ΔBOH:
\(\angle BOH = \frac{\alpha}{2}\) (так как OH — биссектриса);
\(BH = \frac{a}{2}\) (так как OH — медиана);
\(\sin \frac{\alpha}{2} = \frac{BH}{BO} \Rightarrow BO = \frac{a}{\sin \frac{\alpha}{2}} = R\)
5) C = 2πR = \(2π \frac{a}{2 \sin \frac{\alpha}{2}}\)
д)
1) \(S = \frac{1}{2} Pr\)
\(r = R \cdot \cos \frac{180°}{6} = R \cdot \cos 30° = \frac{R\sqrt{3}}{2}\)
\(a_6 = 2R \cdot \sin \frac{180°}{6} = 2R \cdot \sin 30° = R\)
\(P = 6 \cdot R\)
\(S = \frac{1}{2} \cdot 6R \cdot \frac{R\sqrt{3}}{2} = \frac{3\sqrt{3}}{2} R^2\)
2) \(24\sqrt{3} = \frac{3\sqrt{3}}{2} R^2 \Rightarrow R^2 = \frac{16}{3\sqrt{3}} \Rightarrow R = 4 \text{см}\)
3) \(C = 2\pi R = 2 \cdot \pi \cdot 4 = 8\pi \text{см}\)
а) Дано: ΔABC — правильный, AB = a
Решение:
Так как ΔABC — правильный треугольник, то все его стороны равны: AB = BC = AC = a.
Радиус описанной окружности (R) равен половине длины стороны треугольника:
\(R = \frac{a}{2}\)
Длина стороны a_3 равна:
\(a_3 = 2R \cdot \sin 60^\circ = 2 \cdot \frac{a}{2} \cdot \sqrt{3} = a\sqrt{3}\)
Длина окружности (C) равна:
\(C = 2\pi R = 2\pi \cdot \frac{a}{2} = \pi a\)
б) Дано: ΔABC — прямоугольный, ∠C = 90°, AC = a, CB = b
Решение:
Длина гипотенузы AB равна:
\(AB = \sqrt{a^2 + b^2}\)
Радиус описанной окружности (R) равен половине длины гипотенузы:
\(R = \frac{\sqrt{a^2 + b^2}}{2}\)
Длина окружности (C) равна:
\(C = 2\pi R = 2\pi \cdot \frac{\sqrt{a^2 + b^2}}{2} = \pi\sqrt{a^2 + b^2}\)
в) Дано: ΔABC — равнобедренный, AC = a, AB = BC = b
Решение:
1) Пусть OB = R, тогда BM = MC, и OM ⊥ BC.
2) Рассмотрим ΔBHC и ΔOEM: ∠HBC — общий, ∠OEB = ∠BHC = 90°, значит ΔBHC ~ ΔOEM (по 2 углам), OB/BC = BM/BM => OB = BH.
3) Рассмотрим ΔBHC — прямоугольный:
\(BH = \sqrt{BC^2 — HC^2} = \sqrt{b^2 — \left(\frac{a}{2}\right)^2} = \sqrt{b^2 — \frac{a^2}{4}} = \frac{\sqrt{4b^2 — a^2}}{2}\)
4) OB = \(\frac{b \cdot b \cdot 2}{2\sqrt{4b^2 — a^2}} = \frac{b^2}{\sqrt{4b^2 — a^2}} = R\)
5) Длина окружности (C) равна:
\(C = 2\pi R = \frac{2\pi b^2}{\sqrt{4b^2 — a^2}}\)
д) Дано: A₁₄₂₄₃₄₄₄₅₄₆ — правильный шестиугольник; S = 24√3 см²
Решение:
1) Вычислим радиус описанной окружности (R):
\(S = \frac{1}{2} Pr\)
\(r = R \cdot \cos \frac{180°}{6} = R \cdot \cos 30° = \frac{R\sqrt{3}}{2}\)
\(a_6 = 2R \cdot \sin \frac{180°}{6} = 2R \cdot \sin 30° = R\)
\(P = 6 \cdot R\)
\(S = \frac{1}{2} \cdot 6R \cdot \frac{R\sqrt{3}}{2} = \frac{3\sqrt{3}}{2} R^2\)
2) Найдем R:
\(24\sqrt{3} = \frac{3\sqrt{3}}{2} R^2 \Rightarrow R^2 = \frac{16}{3\sqrt{3}} \Rightarrow R = 4 \text{см}\)
3) Длина окружности (C) равна:
\(C = 2\pi R = 2 \cdot \pi \cdot 4 = 8\pi \text{см}\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!