ГДЗ по Геометрии 9 класс Номер 1098 Атанасян — Подробные Ответы

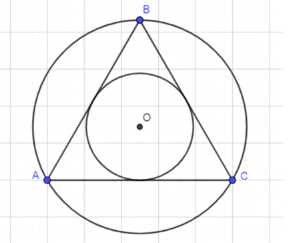
Выразите сторону, периметр и площадь правильного треугольника: а) через радиус вписанной окружности; б) через радиус описанной окружности.

Решение:

a) Через r:
1) r = R · cos(180°/3) = R · cos(60°) = R/2
2) a3 = 2R · sin(180°/3) = 2R · sin(60°) = 2R · √3/2 = 2√3r
3) P = 3 · √(2r) = 6√3r
4) S = (1/2) · P · r = (1/2) · 6√3r · (R/2) = 3√3r²

b) Через R:
1) r = R · cos(180°/3) = R/2
2) a3 = 2R · sin(180°/3) = 2R · √3/2 = √3R
3) P = 3 · √R = 3√3R
4) S = (1/2) · P · r = (1/2) · 3√3R · (R/2) = 3√3R²/4

Ответ:
a) a3 = 2√3r, P = 6√3r, S = 3√3r²
b) a3 = √3R, P = 3√3R, S = 3√3R²/4

Дано:
ΔABC — правильный треугольник;
Окр(0; r); Окр(O; R);

Решение:

a) Выразить a3, P и S через r:

1) Найдем r:
\(r = R \cdot \cos \left(\frac{180^\circ}{3}\right) = R \cdot \cos 60^\circ = \frac{R}{2}\)

2) Найдем a3:
\(a_3 = 2R \cdot \sin \left(\frac{180^\circ}{3}\right) = 2R \cdot \sin 60^\circ = 2R \cdot \frac{\sqrt{3}}{2} = 2\sqrt{3}r\)

3) Найдем P:
\(P = 3 \cdot \sqrt{2r} = 6\sqrt{3}r\)

4) Найдем S:
\(S = \frac{1}{2} \cdot P \cdot r = \frac{1}{2} \cdot 6\sqrt{3}r \cdot \frac{R}{2} = 3\sqrt{3}r^2\)

b) Выразить a3, P и S через R:

1) Найдем r:
\(r = R \cdot \cos \left(\frac{180^\circ}{3}\right) = \frac{R}{2}\)

2) Найдем a3:
\(a_3 = 2R \cdot \sin \left(\frac{180^\circ}{3}\right) = 2R \cdot \frac{\sqrt{3}}{2} = \sqrt{3}R\)

3) Найдем P:
\(P = 3 \cdot \sqrt{R} = 3\sqrt{3}R\)

4) Найдем S:
\(S = \frac{1}{2} \cdot P \cdot r = \frac{1}{2} \cdot 3\sqrt{3}R \cdot \frac{R}{2} = \frac{3\sqrt{3}R^2}{4}\)

Ответ:
a) a3 = 2√3r, P = 6√3r, S = 3√3r²
b) a3 = √3R, P = 3√3R, S = 3√3R²/4