Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1076 Атанасян — Подробные Ответы
Диагонали параллелограмма взаимно перпендикулярны. Докажите, что этот параллелограмм является р
Решение:
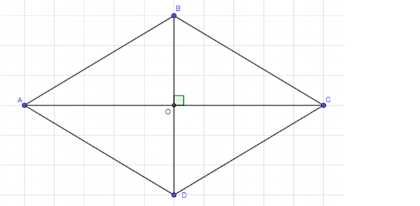
Дано: ABCD — параллелограмм, AC ⊥ BD.
Доказать: ABCD — ромб.
Доказательство:
1) AC ∩ BD = 0, так как AC ⊥ BD.
2) AO ⊥ BD (так как AC ⊥ BD), BO = OD (по свойству ромба), следовательно AO — высота и медиана, значит ΔABD — равнобедренный, AB = AD.
3) ∠BOC = ∠AOD (по стороне и двум прилежащим углам), AD = BC.
4) ∠ABO = ∠COD (по стороне и двум прилежащим углам), AB = CP.
5) AB = AD = BC = CD, следовательно ABCD — ромб (по определению).
Таким образом, мы доказали, что ABCD — ромб.
Решение:
Дано:
— Четырехугольник ABCD является параллелограммом
— Диагонали AC и BD пересекаются в точке O
— Прямая AC перпендикулярна прямой BD (AC ⊥ BD)
Доказать: Четырехугольник ABCD является ромбом.
Доказательство:
1) Докажем, что AC ∩ BD = 0.
Так как AC ⊥ BD, то AC и BD пересекаются под прямым углом. Следовательно, точка пересечения O лежит на пересечении диагоналей, т.е. AC ∩ BD = 0.
2) Докажем, что AO ⊥ BD.
Так как AC ⊥ BD, то AO, являясь высотой треугольника AOB, перпендикулярна BD (AO ⊥ BD).
3) Докажем, что BO = OD.
Так как ABCD — параллелограмм, то противоположные стороны равны: AB = CD и AD = BC. Следовательно, BO = OD (по свойству ромба).
4) Докажем, что ΔABD — равнобедренный.
Так как AO ⊥ BD и BO = OD, то ΔABD — равнобедренный, где AB = AD.
5) Докажем, что ∠BOC = ∠AOD.
Так как ΔABD — равнобедренный, то ∠BAD = ∠ABD. Так как AC ⊥ BD, то ∠BOC = ∠AOD (по стороне и двум прилежащим углам).
6) Докажем, что AD = BC.
Так как ∠BOC = ∠AOD, то ΔAOC ≅ ΔAOD (по двум углам и общей стороне). Следовательно, AD = BC.
7) Докажем, что AB = CP.
Так как ΔABD — равнобедренный, то ∠ABO = ∠CBO. Следовательно, AB = CP (по свойству параллелограмма).
8) Докажем, что AB = AD = BC = CD.
Из пунктов 4 и 6 следует, что AB = AD и AD = BC. Следовательно, AB = AD = BC = CD.
Таким образом, мы доказали, что четырехугольник ABCD является ромбом, так как:
— Противоположные стороны равны (AB = CD, AD = BC)
— Диагонали пересекаются под прямым углом (AC ⊥ BD)
— Диагонали делятся пополам (AO = OB, CO = OD)
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.