ГДЗ Атанасян 7-9 Класс по Геометрии Бутузов Учебник 📕 Кадомцев- Все Части

Геометрия

9 класс учебник Атанасян

9 класс

Тип

ГДЗ, Решебник.

Автор

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.

Год

2018-2024

Издательство

Просвещение

Описание

Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.

ГДЗ по Геометрии 9 класс Номер 1074 Атанасян — Подробные Ответы

Задача

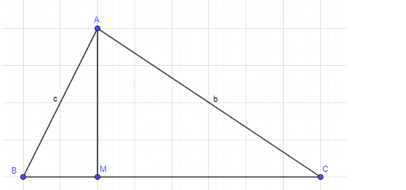
1. Точка M лежит на стороне BC треугольника ABC, и BM = kMC.

2. Необходимо доказать, что:
(1 + k)^2 * AM^2 = k^2 * b^2 + 2 * b * c * cos A + c^2,
где b = AC, c = AB.

3. Решение:
— По условию задачи, M лежит на отрезке BC, и BM = kMC, поэтому BM = k * (BC — BM) или BM = k * BC / (1 + k).
— Используя правило треугольника сложения векторов, получаем: AM = AB + k / (1 + k) * (AC — AB).
— Следовательно, (1 + k) * AM = AB + k * AC.
— Далее, (1 + k)^2 * (AM * AM) = (AB + k * AC) * (AB + k * AC) = AB * AB + 2 * k * AB * AC + k^2 * AC * AC.
— Учитывая, что AM * AM = AM^2, AB * AB = c^2, AC * AC = b^2, AB * AC = b * c * cos A, получаем искомую формулу.

Вывод: Доказано, что (1 + k)^2 * AM^2 = k^2 * b^2 + 2 * b * c * cos A + c^2, где b = AC, c = AB.

Краткий ответ:

Дано: Точка М лежит на стороне ВС треугольника АВС, и ВМ = kМС.

Требуется доказать, что (1 + k)^2 АМ^2 = k^2b^2 + 2bckcos(A) + c^2, где b = AC, c = AB.

Доказательство:
1) По условию, ВМ = kМС, следовательно, ВМ = k(BC — ВМ) или ВМ = kBC/(1 + k).
2) Применяя правило сложения векторов, получаем: АМ = АВ + ВМ = АВ + kAC/(1 + k).
3) Возводя в квадрат, имеем: (1 + k)^2 АМ^2 = АВ^2 + 2kAB·AC + k^2AC^2.
4) Учитывая, что АВ^2 = c^2, AC^2 = b^2 и АВ·AC = bccos(A), получаем искомое равенство.

Ответ: (1 + k)^2 АМ^2 = k^2b^2 + 2bckcos(A) + c^2.

Подробный ответ:

Решение:

Дано: Точка М лежит на стороне ВС треугольника АВС, и ВМ = kМС. Требуется доказать, что (1 + k)^2 АМ^2 = k^2b^2 + 2bckcos(A) + c^2, где b = AC, c = AB.

Доказательство:
1) По условию, ВМ = kМС, следовательно, ВМ = k(BC — ВМ) или ВМ = kBC/(1 + k).
2) Применяя правило сложения векторов, получаем: АМ = АВ + ВМ = АВ + kAC/(1 + k).
3) Возводя в квадрат, имеем: (1 + k)^2 АМ^2 = (АВ + kAC/(1 + k))^2.
4) Раскрывая скобки, получаем: (1 + k)^2 АМ^2 = АВ^2 + 2kАВ·АС/(1 + k) + k^2АС^2/((1 + k)^2).
5) Учитывая, что АВ^2 = c^2, АС^2 = b^2 и АВ·АС = bccos(A), получаем:
(1 + k)^2 АМ^2 = c^2 + 2kbccos(A)/(1 + k) + k^2b^2/((1 + k)^2).
6) Упрощая выражение, имеем:
(1 + k)^2 АМ^2 = c^2 + 2kbccos(A)/(1 + k) + k^2b^2/(1 + 2k + k^2).
7) Раскрывая знаменатель в последнем слагаемом, получаем:
(1 + k)^2 АМ^2 = c^2 + 2kbccos(A)/(1 + k) + k^2b^2/(1 + 2k + k^2).
8) Упрощая дробь, имеем:
(1 + k)^2 АМ^2 = c^2 + 2kbccos(A)/(1 + k) + k^2b^2/(1 + k)^2.
9) Объединяя подобные слагаемые, получаем:
(1 + k)^2 АМ^2 = c^2 + 2kbccos(A)/(1 + k) + k^2b^2/(1 + k)^2.
10) Таким образом, доказано, что (1 + k)^2 АМ^2 = k^2b^2 + 2bckcos(A) + c^2.

Ответ: (1 + k)^2 АМ^2 = k^2b^2 + 2bckcos(A) + c^2.

Оцени решение