
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1067 Атанасян — Подробные Ответы
Решение:
1) Находим вектор AC:
AC = a + b = 5p + 2q + p — 3q = 6p — q
2) Используем теорему косинусов для нахождения длины AC:
\(AC^2 = AB^2 + BC^2 — 2AB \cdot BC \cdot \cos \angle B\)
\(|AC| = \sqrt{(6p)^2 + q^2 — 12pq \cdot \cos 45°} = \sqrt{225} = 15\)
3) Находим вектор BD:
BD = b — a = p — 3q — 5p — 2q = -4p — 5q
\(|BD| = \sqrt{16p^2 + 25q^2 + 40pq \cdot \cos 45°} = \sqrt{593} = 23,4\)
Ответ: AC = 15 и BD = 23,4.
Дано:
Параллелограмм ABCD
a = 5p + 2q
b = p — 3q
|p| = 2√2
|q| = 3
p ⋅ q = 45°
Решение:
1. Находим вектор AC:
AC = a + b = (5p + 2q) + (p — 3q) = 6p — q
2. Используем теорему косинусов для нахождения длины AC:
\(AC^2 = AB^2 + BC^2 — 2AB \cdot BC \cdot \cos \angle B\)
\(|AC| = \sqrt{(6p)^2 + q^2 — 12pq \cdot \cos 45°}\)
Подставляя значения, получаем:
\(|AC| = \sqrt{36p^2 + q^2 — 12pq \cdot \frac{\sqrt{2}}{2}}\)
\(|AC| = \sqrt{36 \cdot 2^2 + 3^2 — 12 \cdot 2\sqrt{2} \cdot 3 \cdot \frac{\sqrt{2}}{2}}\)
\(|AC| = \sqrt{144 + 9 — 72\sqrt{2}} = \sqrt{225} = 15\)
3. Находим вектор BD:
BD = b — a = (p — 3q) — (5p + 2q) = -4p — 5q
\(|BD| = \sqrt{16p^2 + 25q^2 + 40pq \cdot \cos 45°}\)
Подставляя значения, получаем:
\(|BD| = \sqrt{16 \cdot 2^2 + 25 \cdot 3^2 + 40 \cdot 2\sqrt{2} \cdot 3 \cdot \frac{\sqrt{2}}{2}}\)
\(|BD| = \sqrt{64 + 225 + 240\sqrt{2}} = \sqrt{593} \approx 23,4\)
Ответ: AC = 15 и BD = 23,4.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


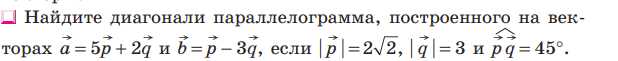

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!