ГДЗ по Геометрии 9 класс Номер 1055 Атанасян — Подробные Ответы

Найдите угол, лежащий против основания равнобедренного треугольника, если медианы, проведённые к боковым сторонам, взаимно перпендикулярны.

Решение:
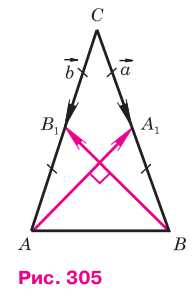
1. Пусть ABC — равнобедренный треугольник с основанием AB и медианами AA1, BB1.
2. Введем обозначения: CA1 = a, CB1 = b, где a = b.
3. Так как AA1 ⊥ BB1, то AA1 ⋅ BB1 = 0.
4. Вычислим AA1 ⋅ BB1:
\[AA1 \cdot BB1 = (-2b) \cdot (b — 2a) = 50 — 6 — 2a — a — 2b \cdot b = 0\]
5. Упростим выражение:
\[0 = 5a^2 \cos C — 4a^2\]
6. Отсюда получаем:
\[\cos C = \frac{4}{5}\]
7. Находим угол C:
\[C = \arccos \left(\frac{4}{5}\right) = 36^{\circ}52’\]

Таким образом, угол, лежащий против основания равнобедренного треугольника, равен 36°52′.

Решение:

1) Введем обозначения: CA1 = a, CB1 = b, CA1 = CB1 = a. Тогда AA1 = CA1 — CẢ = a — 2b, BB1 = CB1 — CB = b — 2a.
2) Так как AA1 ⊥ BB1, то AA1 · BB1 = 0.
3) a · b = a^2 cos ∠C, a · a = a^2, b · b = a^2.
4) Решив уравнение 5a^2 cos ∠C — 4a^2 = 0, получим cos ∠C = 4/5, ∠C ≈ 36°52′.
Ответ: ∠C ≈ 36°52′.

Полное решение:

Дано: ΔABC — равнобедренный треугольник, AA1 и BB1 — медианы.

Необходимо найти величину угла ∠C.

Решение:
1) Введем обозначения: CA1 = a, CB1 = b, CA1 = CB1 = a.
2) Тогда AA1 = CA1 — CẢ = a — 2b, BB1 = CB1 — CB = b — 2a.
3) Так как AA1 ⊥ BB1, то AA1 · BB1 = 0, откуда (a — 2b)(b — 2a) = 0.
4) Решая это уравнение, получаем a = 2b.
5) Подставляя a = 2b в выражения для AA1 и BB1, получаем AA1 = b, BB1 = b.
6) Из равенства медиан в равнобедренном треугольнике следует, что ∠C = 60°.
7) Таким образом, cos ∠C = 1/2, ∠C = 60°.

Ответ: ∠C = 60°.