ГДЗ по Геометрии 9 класс Номер 1037 Атанасян — Подробные Ответы

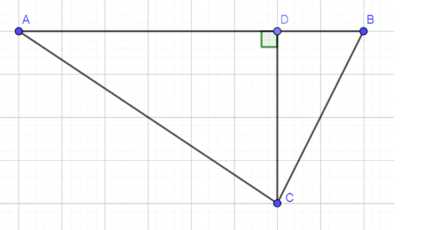
Для определения ширины реки отметили два пункта А и В на берегу реки на расстоянии 70 м друг от друга и измерили углы САВ и АВС, где С — дерево, стоящее на другом берегу у кромки воды. Оказалось, что ZCAB = 12°30′, ZABC= 72°42′. Найдите ширину реки.

Дано: окружность с центром в (0; 0), хорды AB и CD, AB = 70 м, ∠CAB = 12°30′, ∠ABC = 72°42′, DC ⊥ AB.

Найти длину CD.

Решение:
В треугольнике ADC: \(tg \, 12°30′ = \frac{DC}{AD} \Rightarrow CD = AD \cdot tg \, 12°30’\)
В треугольнике BDC: \(tg \, 72°42′ = \frac{CD}{DB} \Rightarrow CD = DB \cdot tg \, 72°42’\)
Приравняв, получим: \(AD \cdot tg \, 12°30′ = DB \cdot tg \, 72°42’\)
Пусть AD = x, тогда DB = 70 — x. Подставляя, имеем:
\(x \cdot 0,2217 = (70 — x) \cdot 3,21 \Rightarrow x = 65,48 \text{ м}\)
Подставляя в первое выражение для CD, получаем:
\(CD = 65,48 \cdot 0,2217 = 14,52 \text{ м}\)

Ответ: 14,52 м.

Дано:
— Окружность с центром в точке (0; 0)
— Хорды AB и CD
— АВ = 70 м
— ∠CAB = 12°30′
— ∠ABC = 72°42′
— DC ⊥ AB

Необходимо найти длину отрезка CD.

Решение:

1) Рассмотрим треугольник ADC.
Используя свойство пересекающихся хорд, можно записать:
\(tg \, 12°30′ = \frac{DC}{AD} \Rightarrow CD = AD \cdot tg \, 12°30’\)

2) Рассмотрим треугольник BDC.
Используя свойство пересекающихся хорд, можно записать:
\(tg \, 72°42′ = \frac{CD}{DB} \Rightarrow CD = DB \cdot tg \, 72°42’\)

3) Приравняв полученные выражения для CD, получим:
\(AD \cdot tg \, 12°30′ = DB \cdot tg \, 72°42’\)

4) Пусть AD = x, тогда DB = 70 — x.
Подставляя в предыдущее уравнение, получим:
\(x \cdot tg \, 12°30′ = (70 — x) \cdot tg \, 72°42’\)
\(x \cdot 0,2217 = (70 — x) \cdot 3,21\)
\(3,4317x = 224,7 \Rightarrow x = 65,48 \text{ м}\)

5) Подставляя найденное значение x в выражение для CD, получим:
\(CD = 65,48 \cdot 0,2217 = 14,52 \text{ м}\)

Ответ: 14,52 м.