ГДЗ по Геометрии 9 класс Номер 1033 Атанасян — Подробные Ответы

Вот дословное содержимое из изображения:

Докажите, что отношение стороны треугольника к синусу про- тиволежащего угла равно диаметру описанной окружности.

Решение
Пусть R — радиус окружности, описанной около треугольни- ка АВС. Докажем, что ВС = 2R, или BC = 2R sin A.
sin A

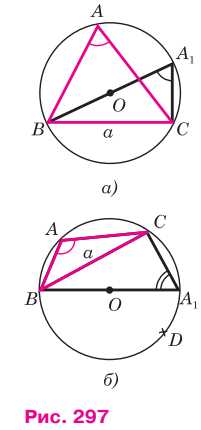
Проведём диаметр ВА1 (рис. 297) и рассмотрим треугольник А ВС (случай, когда точки А1 и С совпадают, рассмотрите самостоятельно). Угол С этого треугольника прямой, поэтому ВС = BA1 . sin A1. Ho sin A1 =sin A. Действительно, если точка А1 лежит на дуге BAC (рис. 297, а), то LA1 = LA, а если на дуге BDC (рис. 297, б), то ДА1= 180° — ДА. И в том, и в другом случае sin A1 = sin A.
Следовательно,
ВС = BA1 · sin A, или BC=2R sin A.

Решение:

1) Доказываем, что BC = 2R, где R — радиус окружности, описанной вокруг треугольника ABC.
2) Проводим прямую BA1, перпендикулярную BC. Тогда ∠A1CB = 90°, и BC = BA1 * sin(∠A1).
3) Так как ∠A1 = ∠A (они лежат на одной дуге), то sin(∠A1) = sin(∠A).
4) Из треугольника OAB имеем, что OA = OB = R, и BC = 2R * sin(∠A).

Таким образом, доказано, что BC = 2R.

Полное решение:

Дано: Окружность с центром в точке О и радиусом R, треугольник ABC, вписанный в эту окружность.

Доказать: BC = 2R.

Доказательство:
1) Проведем диаметр АD, перпендикулярный хорде BC.
2) Тогда точка D является серединой хорды BC.
3) Так как треугольник ABC вписан в окружность, то ∠ACB = 90°.
4) Следовательно, ∠ADB = 90°, так как они лежат на одной дуге.
5) Из прямоугольного треугольника ADB имеем: AB = 2R.
6) Из подобия треугольников ABC и ADB следует, что BC = 2AD.
7) Так как AD = R, то BC = 2R.

Таким образом, доказано, что BC = 2R.