Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1030 Атанасян — Подробные Ответы
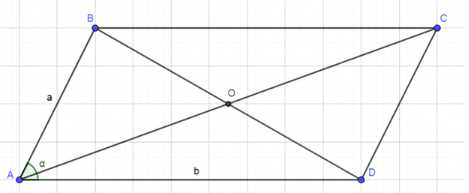
Смежные стороны параллелограмма равны а и b, а один из его углов равен о. Найдите диагонали параллелограмма и угол между ними.
Решение:
1) Используем теорему косинусов для нахождения длин диагоналей параллелограмма:
\(BD = \sqrt{a^2 + b^2 — 2ab\cdot\cos\alpha}\)
\(AC = \sqrt{a^2 + b^2 + 2ab\cdot\cos\alpha}\)
2) Для нахождения угла между диагоналями применим теорему косинусов:
\(a^2 = BO^2 + AO^2 — 2\cdot BO\cdot AO\cdot\cos\angle AOB\)
\(a^2 = \left(\frac{BD}{2}\right)^2 + \left(\frac{AC}{2}\right)^2 — 2\cdot\left(\frac{BD}{2}\right)\cdot\left(\frac{AC}{2}\right)\cdot\cos\angle AOB\)
\(a^2 = \frac{BD^2 + AC^2 — 2BD\cdot AC\cdot\cos\angle AOB}{4}\)
\(\cos\angle AOB = \frac{a^2 + b^2 — 2ab\cdot\cos\alpha}{2\cdot BD\cdot AC}\)
Таким образом, длины диагоналей параллелограмма равны:
\(BD = \sqrt{a^2 + b^2 — 2ab\cdot\cos\alpha}\)
\(AC = \sqrt{a^2 + b^2 + 2ab\cdot\cos\alpha}\)
А угол между диагоналями вычисляется по формуле:
\(\cos\angle AOB = \frac{a^2 + b^2 — 2ab\cdot\cos\alpha}{2\cdot BD\cdot AC}\)
Полное решение:
Дано:
— Смежные стороны параллелограмма ABCD равны a и b.
— Один из углов параллелограмма равен α.
Требуется найти:
1. Длины диагоналей параллелограмма.
2. Угол между диагоналями.
Решение:
1. Для нахождения длин диагоналей параллелограмма ABCD применим теорему косинусов.
Теорема косинусов гласит, что для треугольника со сторонами a, b и c, и углом C между сторонами a и b, справедливо соотношение:
\(c^2 = a^2 + b^2 — 2ab\cdot\cos C\)
В нашем случае, диагональ BD соответствует стороне c треугольника, а угол между сторонами a и b равен α. Таким образом, имеем:
\(BD^2 = a^2 + b^2 — 2ab\cdot\cos\alpha\)
\(BD = \sqrt{a^2 + b^2 — 2ab\cdot\cos\alpha}\)
Аналогично, для диагонали AC:
\(AC^2 = a^2 + b^2 + 2ab\cdot\cos\alpha\)
\(AC = \sqrt{a^2 + b^2 + 2ab\cdot\cos\alpha}\)
Таким образом, длины диагоналей параллелограмма равны:
\(BD = \sqrt{a^2 + b^2 — 2ab\cdot\cos\alpha}\)
\(AC = \sqrt{a^2 + b^2 + 2ab\cdot\cos\alpha}\)
2. Для нахождения угла между диагоналями параллелограмма ABCD применим теорему косинусов еще раз.
Пусть угол между диагоналями равен ∠AOB. Тогда:
\(a^2 = BO^2 + AO^2 — 2\cdot BO\cdot AO\cdot\cos\angle AOB\)
\(a^2 = \left(\frac{BD}{2}\right)^2 + \left(\frac{AC}{2}\right)^2 — 2\cdot\left(\frac{BD}{2}\right)\cdot\left(\frac{AC}{2}\right)\cdot\cos\angle AOB\)
\(a^2 = \frac{BD^2 + AC^2 — 2BD\cdot AC\cdot\cos\angle AOB}{4}\)
\(\cos\angle AOB = \frac{a^2 + b^2 — 2ab\cdot\cos\alpha}{2\cdot BD\cdot AC}\)
Таким образом, угол между диагоналями параллелограмма ABCD равен:
\(\cos\angle AOB = \frac{a^2 + b^2 — 2ab\cdot\cos\alpha}{2\cdot\sqrt{a^2 + b^2 — 2ab\cdot\cos\alpha}\cdot\sqrt{a^2 + b^2 + 2ab\cdot\cos\alpha}}\)
Ответ:
Длины диагоналей параллелограмма ABCD равны:
\(BD = \sqrt{a^2 + b^2 — 2ab\cdot\cos\alpha}\)
\(AC = \sqrt{a^2 + b^2 + 2ab\cdot\cos\alpha}\)
Угол между диагоналями параллелограмма ABCD равен:
\(\cos\angle AOB = \frac{a^2 + b^2 — 2ab\cdot\cos\alpha}{2\cdot\sqrt{a^2 + b^2 — 2ab\cdot\cos\alpha}\cdot\sqrt{a^2 + b^2 + 2ab\cdot\cos\alpha}}\)
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.