Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1029 Атанасян — Подробные Ответы
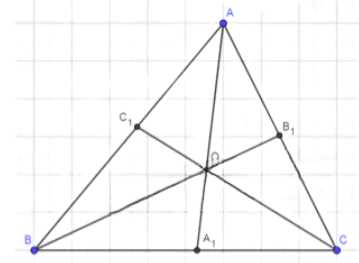
Найдите биссектрисы треугольника, если одна из его сторон равна а, а прилежащие к этой стороне углы равны α и β.
Решение:
1) Рассмотрим ∆BBB1C:
∠BBB1C = 180° — ∠B — ∠B = 180° — 2β
По теореме синусов:
BB1 = a·sin(2β) / sin(β)
2) Рассмотрим ∆ABC1:
∠ABC1 = 180° — α — β/2
По теореме синусов:
CC1 = a·sin(α) / sin(α + β/2)
3) Рассмотрим ∆BAA1:
∠BAA1 = 90° — β/2
∠BAA1 = 90° + β/2 — α
По теореме синусов:
AA1 = a·sin(α) / sin(90° + β/2 — α)
Ответы:
CC1 = a·sin(α) / sin(α + β/2)
BB1 = a·sin(2β) / sin(β)
AA1 = a·sin(α) / sin(90° + β/2 — α)
Решение:
Дано: параллелограмм ABCD, где AD = 7/3 м, BD = 4,4 м, ∠A = 22°30′.
Найти: ∠BDC и ∠DBC.
1) Рассмотрим треугольник ∆ABC:
По теореме косинусов:
AB² = AD² + BC² — 2·AD·BC·cos(∠A)
AB² = (7/3)² + BC² — 2·(7/3)·BC·cos(22°30′)
AB² = 49/9 + BC² — 4,67·BC·cos(22°30′)
AB = √(49/9 + BC² — 4,67·BC·cos(22°30′))
2) Рассмотрим треугольник ∆BDC:
По теореме косинусов:
BC² = BD² + DC² — 2·BD·DC·cos(∠BDC)
BC² = 4,4² + DC² — 2·4,4·DC·cos(∠BDC)
BC² = 19,36 + DC² — 8,8·DC·cos(∠BDC)
3) Приравняем выражения для BC² из пунктов 1 и 2:
49/9 + BC² — 4,67·BC·cos(22°30′) = 19,36 + DC² — 8,8·DC·cos(∠BDC)
BC² — DC² = 49/9 — 19,36 + 4,67·BC·cos(22°30′) — 8,8·DC·cos(∠BDC)
BC² — DC² = 29/9 + 4,67·BC·cos(22°30′) — 8,8·DC·cos(∠BDC)
4) Решим полученное уравнение относительно ∠BDC:
cos(∠BDC) = (29/9 + 4,67·BC·cos(22°30′)) / (8,8·DC)
5) Найдем ∠DBC:
∠DBC = 180° — ∠A — ∠BDC
Ответы:
∠BDC = arccos((29/9 + 4,67·BC·cos(22°30′)) / (8,8·DC))
∠DBC = 180° — 22°30′ — ∠BDC
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.