
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1028 Атанасян — Подробные Ответы
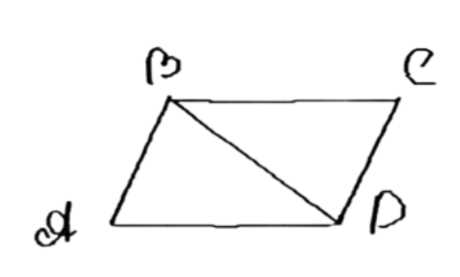
В параллелограмме ABCD AD = 7/3 м, BD = 4,4 м, ∠A = 22°30′. Найдите ∠BDC и ∠DBC.
Решение:
1) Используем теорему синусов для ΔABD:
sin(∠A) / AB = sin(∠ABD) / BD = sin(∠ADB) / AD
Подставляем известные значения:
sin(22°30′) / 4.4 = sin(∠ADB) / 75
∠ADB = 39°38′
2) Находим ∠ADB = 180° — (39°38′ + 22°30′) = 117°52′
3) ∠BDC = ∠ABD = 39°38′
Таким образом, решение задачи сводится к применению теоремы синусов и вычислению углов треугольника.
Полное решение задачи:
Дано: четырехугольник ABCD, где AB = 22,5 м, BC = 7 1/3 м, AD = 75 м, BD = 4,4 м, ∠A = 22°30′.
Решение:
1) Применим теорему синусов для треугольника ABD:
sin(∠A) / AB = sin(∠ABD) / BD
Подставляя известные значения, получим:
sin(22°30′) / 22,5 = sin(∠ABD) / 4,4
∠ABD = 39°38′
2) Найдем угол ∠ADB:
∠ADB = 180° — (∠A + ∠ABD)
∠ADB = 180° — (22°30′ + 39°38′) = 117°52′
3) Так как ABCD — параллелограмм, то ∠BDC = ∠ABD = 39°38′.
Ответ:
∠ADB = 117°52′
∠BDC = 39°38′
Таким образом, задача решена с применением теоремы синусов и свойств параллелограмма.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!