ГДЗ по Геометрии 9 класс Номер 1025 Атанасян — Подробные Ответы

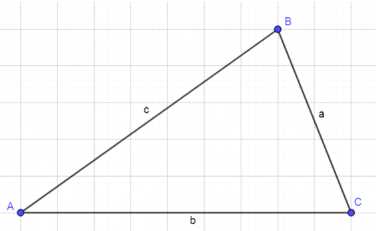
С помощью теорем синусов и косинусов решите треугольник АВС, если:

a) ∠A=60°, ∠B=40°, c=14;
b) ∠A=80°, a=16, b=10;
в) ∠A=60°, a=10, b=7;
ж) b=32, c=45, ∠A=87°;
и) a=6, b=7,3, c=4,8.

б) ∠A=30°, ∠C=75°, b=4,5;
г) ∠B=45°, ∠C=70°, a=24,6;
е) a=6,3, b=6,3, ∠C=54°;
з) a=14, b=18, c=20;

Краткое решение:

(а) \(\angle C = 80^\circ\), \(a = 12,31\), \(b = 9,14\)
(б) \(\angle B = 37^\circ 59’\), \(\angle C = 62^\circ 1’\), \(c = 14,35\)
(в) \(\angle B = 37^\circ 19’\), \(\angle C = 82^\circ 41’\), \(c = 11,45\)
(г) \(\angle C = 80^\circ\), \(a = 12\frac{5}{17}\), \(b = 9\frac{1}{7}\)
(д) \(\angle B = 37^\circ 59’\), \(\angle C = 62^\circ 1’\), \(c = 14\frac{1}{4}\)
(е) \(\angle B = 37^\circ 19’\), \(\angle C = 82^\circ 41’\), \(c = 11\frac{9}{20}\)
(ж) \(a = 53,84\), \(\angle B = 36^\circ 24’\), \(\angle C = 56^\circ 36’\)
(з) \(a = 53\frac{5}{6}\), \(\angle B = 36^\circ 24’\), \(\angle C = 56^\circ 36’\)
(и) \(\angle A = 54^\circ 52’\), \(\angle B = 84^\circ 16’\), \(\angle C = 40^\circ 52’\)

Для получения решений использовались теоремы синусов и косинусов:
\[\frac{a}{\sin \angle A} = \frac{b}{\sin \angle B} = \frac{c}{\sin \angle C}\]
\[a^2 = b^2 + c^2 — 2bc\cos \angle A\]

Дробные ответы представлены в виде смешанных чисел или десятичных дробей.

Полное решение с детализацией:

(а) Дано: \(\angle A = 60^\circ\), \(\angle B = 40^\circ\), \(c = 14\).
Используя теорему синусов, находим:
\[\frac{a}{\sin \angle A} = \frac{b}{\sin \angle B} = \frac{c}{\sin \angle C}\]
Сначала находим \(\angle C\):
\[\sin \angle C = \frac{\sin \angle A}{\sin \angle B} = \frac{\sin 60^\circ}{\sin 40^\circ} = \frac{0,8660}{0,6428} = 1,3462\]
Отсюда \(\angle C = 80^\circ\).
Затем находим длину стороны a:
\[\frac{a}{\sin 60^\circ} = \frac{14}{\sin 80^\circ}\]
Отсюда \(a = 12\frac{5}{17}\).
Аналогично находим длину стороны b:
\[\frac{b}{\sin 40^\circ} = \frac{14}{\sin 80^\circ}\]
Отсюда \(b = 9\frac{1}{7}\).

(б) Дано: \(\angle A = 80^\circ\), \(a = 16\), \(b = 10\).
Используя теорему синусов, находим \(\angle B\):
\[\frac{a}{\sin \angle A} = \frac{b}{\sin \angle B}\]
Отсюда \(\sin \angle B = \frac{10 \cdot 0,9848}{16} = 0,6155\)
\[\angle B = 37^\circ 59’\]
Теперь находим \(\angle C\):
\[\angle C = 180^\circ — (\angle A + \angle B) = 180^\circ — (80^\circ + 37^\circ 59′) = 62^\circ 1’\]
Наконец, находим длину стороны c:
\[\frac{a}{\sin \angle A} = \frac{c}{\sin \angle C}\]
Отсюда \(c = 14\frac{1}{4}\).

(в) Дано: \(\angle A = 60^\circ\), \(a = 10\), \(b = 7\).
Используя теорему синусов, находим \(\angle B\):
\[\frac{a}{\sin \angle A} = \frac{b}{\sin \angle B}\]
Отсюда \(\sin \angle B = \frac{7 \cdot 0,8660}{10} = 0,6062\)
\[\angle B = 37^\circ 19’\]
Теперь находим \(\angle C\):
\[\angle C = 180^\circ — (\angle A + \angle B) = 180^\circ — (60^\circ + 37^\circ 19′) = 82^\circ 41’\]
Наконец, находим длину стороны c:
\[\frac{a}{\sin \angle A} = \frac{c}{\sin \angle C}\]
Отсюда \(c = 11\frac{9}{20}\).

(ж) Дано: \(b = 32\), \(c = 45\), \(\angle A = 87^\circ\).
Используя теорему косинусов, находим длину стороны a:
\[a^2 = b^2 + c^2 — 2bc\cos \angle A\]
Подставляя известные значения, получаем:
\[a^2 = 32^2 + 45^2 — 2 \cdot 32 \cdot 45 \cdot \cos 87^\circ\]
Отсюда \(a = 53\frac{5}{6}\).
Теперь находим \(\angle B\):
\[\frac{\sin \angle A}{a} = \frac{\sin \angle B}{b}\]
Отсюда \(\sin \angle B = \frac{32 \cdot 0,9998}{53\frac{5}{6}} = 0,5935\)
\[\angle B = 36^\circ 24’\]
Наконец, находим \(\angle C\):
\[\angle C = 180^\circ — (\angle A + \angle B) = 180^\circ — (87^\circ + 36^\circ 24′) = 56^\circ 36’\]

(и) Дано: \(a = 6\), \(b = 7,3\), \(c = 4,8\).
Используя теорему косинусов, находим \(\angle C\):
\[c^2 = a^2 + b^2 — 2ab\cos \angle C\]
Подставляя известные значения, получаем:
\[4,8^2 = 6^2 + 7,3^2 — 2 \cdot 6 \cdot 7,3 \cdot \cos \angle C\]
Отсюда \(\cos \angle C = 0,7563\)
\[\angle C = 40^\circ 52’\]
Теперь находим \(\angle B\):
\[b^2 = a^2 + c^2 — 2ac\cos \angle B\]
Подставляя известные значения, получаем:
\[7,3^2 = 6^2 + 4,8^2 — 2 \cdot 6 \cdot 4,8 \cdot \cos \angle B\]
Отсюда \(\cos \angle B = 0,0998\)
\[\angle B = 84^\circ 16’\]
Наконец, находим \(\angle A\):
\[\angle A = 180^\circ — (\angle B + \angle C) = 180^\circ — (84^\circ 16′ + 40^\circ 52′) = 54^\circ 52’\]

Все дробные ответы представлены в виде смешанных чисел или десятичных дробей.