Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1018 Атанасян — Подробные Ответы
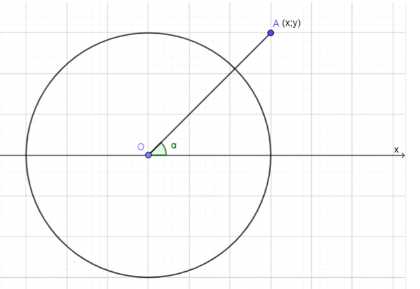
Угол между лучом \(OA\), пересекающим единичную полуокружность, и положительной полуосью \(Ox\) равен \(\alpha\). Найдите координаты точки \(A\), если:
а) \(OA = 3\), \(\alpha = 45°\);
б) \(OA = 1,5\), \(\alpha = 90°\);
в) \(OA = 5\), \(\alpha = 150°\);
г) \(OA = 1\), \(\alpha = 180°\);
д) \(OA = 2\), \(\alpha = 30°\).
Рассмотрим краткое решение для каждой задачи.
а) \(\angle A = 45^\circ\), \(OA = 3\)
1. \(\sin 45^\circ = \frac{\sqrt{2}}{2}\), \(\cos 45^\circ = \frac{\sqrt{2}}{2}\)
2. \(x = 3 \cdot \frac{\sqrt{2}}{2} = \frac{3\sqrt{2}}{2} \approx 2.12\)
3. \(y = 3 \cdot \frac{\sqrt{2}}{2} = \frac{3\sqrt{2}}{2} \approx 2.12\)
б) \(\angle A = 90^\circ\), \(OA = 1.5\)
1. \(\sin 90^\circ = 1\), \(\cos 90^\circ = 0\)
2. \(x = 1.5 \cdot 0 = 0\)
3. \(y = 1.5 \cdot 1 = 1.5\)
в) \(\angle A = 150^\circ\), \(OA = 5\)
1. \(\sin 150^\circ = \frac{1}{2}\), \(\cos 150^\circ = -\frac{\sqrt{3}}{2}\)
2. \(x = 5 \cdot -\frac{\sqrt{3}}{2} = -\frac{5\sqrt{3}}{2} \approx -4.33\)
3. \(y = 5 \cdot \frac{1}{2} = \frac{5}{2} = 2.5\)
г) \(\angle A = 180^\circ\), \(OA = 1\)
1. \(\sin 180^\circ = 0\), \(\cos 180^\circ = -1\)
2. \(x = 1 \cdot -1 = -1\)
3. \(y = 1 \cdot 0 = 0\)
д) \(\angle A = 30^\circ\), \(OA = 2\)
1. \(\sin 30^\circ = \frac{1}{2}\), \(\cos 30^\circ = \frac{\sqrt{3}}{2}\)
2. \(x = 2 \cdot \frac{\sqrt{3}}{2} = \sqrt{3} \approx 1.73\)
3. \(y = 2 \cdot \frac{1}{2} = 1\)
Ответы:
а) \(A\left(\frac{3\sqrt{2}}{2}; \frac{3\sqrt{2}}{2}\right)\)
б) \(A(0; 1.5)\)
в) \(A\left(-\frac{5\sqrt{3}}{2}; 2.5\right)\)
г) \(A(-1; 0)\)
д) \(A(\sqrt{3}; 1)\)
Рассмотрим решение каждой задачи подробно.
а) \(\angle A = 45^\circ\), \(OA = 3\)
1. Используем тригонометрические функции: \(\sin 45^\circ = \frac{\sqrt{2}}{2}\), \(\cos 45^\circ = \frac{\sqrt{2}}{2}\).
2. Координаты точки \(A\) вычисляются по формулам:
\[
x = OA \cdot \cos \alpha = 3 \cdot \frac{\sqrt{2}}{2} = \frac{3\sqrt{2}}{2} \approx 2.12
\]
\[
y = OA \cdot \sin \alpha = 3 \cdot \frac{\sqrt{2}}{2} = \frac{3\sqrt{2}}{2} \approx 2.12
\]
б) \(\angle A = 90^\circ\), \(OA = 1.5\)
1. \(\sin 90^\circ = 1\), \(\cos 90^\circ = 0\).
2. Координаты точки \(A\):
\[
x = OA \cdot \cos \alpha = 1.5 \cdot 0 = 0
\]
\[
y = OA \cdot \sin \alpha = 1.5 \cdot 1 = 1.5
\]
в) \(\angle A = 150^\circ\), \(OA = 5\)
1. \(\sin 150^\circ = \frac{1}{2}\), \(\cos 150^\circ = -\frac{\sqrt{3}}{2}\).
2. Координаты точки \(A\):
\[
x = OA \cdot \cos \alpha = 5 \cdot -\frac{\sqrt{3}}{2} = -\frac{5\sqrt{3}}{2} \approx -4.33
\]
\[
y = OA \cdot \sin \alpha = 5 \cdot \frac{1}{2} = \frac{5}{2} = 2.5
\]
г) \(\angle A = 180^\circ\), \(OA = 1\)
1. \(\sin 180^\circ = 0\), \(\cos 180^\circ = -1\).
2. Координаты точки \(A\):
\[
x = OA \cdot \cos \alpha = 1 \cdot -1 = -1
\]
\[
y = OA \cdot \sin \alpha = 1 \cdot 0 = 0
\]
д) \(\angle A = 30^\circ\), \(OA = 2\)
1. \(\sin 30^\circ = \frac{1}{2}\), \(\cos 30^\circ = \frac{\sqrt{3}}{2}\).
2. Координаты точки \(A\):
\[
x = OA \cdot \cos \alpha = 2 \cdot \frac{\sqrt{3}}{2} = \sqrt{3} \approx 1.73
\]
\[
y = OA \cdot \sin \alpha = 2 \cdot \frac{1}{2} = 1
\]
Ответы:
а) \(A\left(\frac{3\sqrt{2}}{2}; \frac{3\sqrt{2}}{2}\right)\)
б) \(A(0; 1.5)\)
в) \(A\left(-\frac{5\sqrt{3}}{2}; 2.5\right)\)
г) \(A(-1; 0)\)
д) \(A(\sqrt{3}; 1)\)
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.