
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1017 Атанасян — Подробные Ответы
Постройте ∠A, если:
а) sin A = \(\frac{2}{3}\);
б) cos A = \(\frac{3}{4}\);
в) cos A = \(-\frac{2}{5}\).
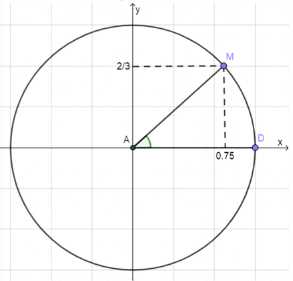
а) \(\sin \angle A = \frac{2}{3}\)
1. Начертим единичную окружность.
2. Используем равенство \(\sin^2 \angle A + \cos^2 \angle A = 1\).
3. \(\left(\frac{2}{3}\right)^2 + \cos^2 \angle A = 1\) \(\Rightarrow \cos^2 \angle A = 1 — \frac{4}{9} = \frac{5}{9}\).
4. \(\cos \angle A = \frac{\sqrt{5}}{3} \approx 0.75\).
5. Координаты: \(x_M = 0.75\), \(y_M = \frac{2}{3}\).
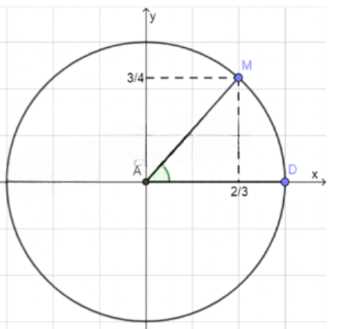
б) \(\cos \angle A = \frac{3}{4}\)
1. Начертим единичную окружность.
2. Используем равенство \(\sin^2 \angle A + \cos^2 \angle A = 1\).
3. \(\sin^2 \angle A + \left(\frac{3}{4}\right)^2 = 1\) \(\Rightarrow \sin^2 \angle A = 1 — \frac{9}{16} = \frac{7}{16}\).
4. \(\sin \angle A = \frac{\sqrt{7}}{4} \approx 0.66\).
5. Координаты: \(x_M = \frac{2}{3}\), \(y_M = \frac{3}{4}\).
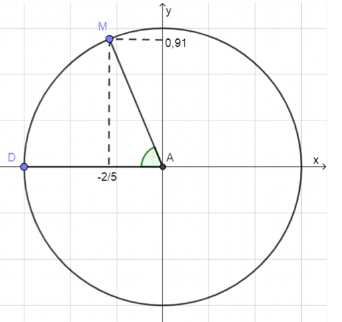
в) \(\cos \angle A = -\frac{2}{5}\)
1. Начертим единичную окружность.
2. Используем равенство \(\sin^2 \angle A + \cos^2 \angle A = 1\).
3. \(\sin^2 \angle A + \left(-\frac{2}{5}\right)^2 = 1\) \(\Rightarrow \sin^2 \angle A = 1 — \frac{4}{25} = \frac{21}{25}\).
4. \(\sin \angle A = \frac{\sqrt{21}}{5} \approx 0.91\).
5. Координаты: \(x_M = -\frac{2}{5}\), \(y_M = 0.91\).
а) \(\sin \angle A = \frac{2}{3}\)
1. Начертим единичную окружность, где радиус равен 1.
2. Используем основное тригонометрическое тождество: \(\sin^2 \angle A + \cos^2 \angle A = 1\).
3. Подставляем известное значение: \(\left(\frac{2}{3}\right)^2 + \cos^2 \angle A = 1\).
4. Вычисляем: \(\frac{4}{9} + \cos^2 \angle A = 1\).
5. \(\cos^2 \angle A = 1 — \frac{4}{9} = \frac{5}{9}\).
6. \(\cos \angle A = \sqrt{\frac{5}{9}} = \frac{\sqrt{5}}{3} \approx 0.75\).
7. Координаты точки \(M\) на окружности: \(x_M = 0.75\), \(y_M = \frac{2}{3}\).
б) \(\cos \angle A = \frac{3}{4}\)
1. Начертим единичную окружность.
2. Используем основное тригонометрическое тождество: \(\sin^2 \angle A + \cos^2 \angle A = 1\).
3. Подставляем известное значение: \(\sin^2 \angle A + \left(\frac{3}{4}\right)^2 = 1\).
4. Вычисляем: \(\sin^2 \angle A + \frac{9}{16} = 1\).
5. \(\sin^2 \angle A = 1 — \frac{9}{16} = \frac{7}{16}\).
6. \(\sin \angle A = \sqrt{\frac{7}{16}} = \frac{\sqrt{7}}{4} \approx 0.66\).
7. Координаты точки \(M\) на окружности: \(x_M = \frac{3}{4}\), \(y_M = 0.66\).
в) \(\cos \angle A = -\frac{2}{5}\)
1. Начертим единичную окружность.
2. Используем основное тригонометрическое тождество: \(\sin^2 \angle A + \cos^2 \angle A = 1\).
3. Подставляем известное значение: \(\sin^2 \angle A + \left(-\frac{2}{5}\right)^2 = 1\).
4. Вычисляем: \(\sin^2 \angle A + \frac{4}{25} = 1\).
5. \(\sin^2 \angle A = 1 — \frac{4}{25} = \frac{21}{25}\).
6. \(\sin \angle A = \sqrt{\frac{21}{25}} = \frac{\sqrt{21}}{5} \approx 0.91\).
7. Координаты точки \(M\) на окружности: \(x_M = -0.4\), \(y_M = 0.91\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!