
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1012 Атанасян — Подробные Ответы
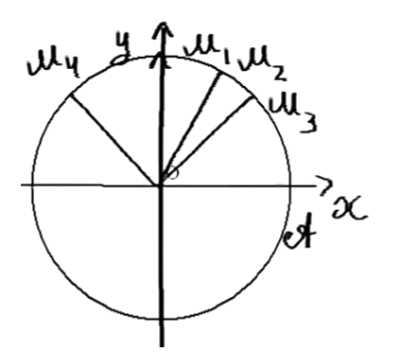
Проверьте, что точки \(M_1 (0; 1)\), \(M_2 \left(\frac{1}{2}; \frac{\sqrt{3}}{2}\right)\), \(M_3 \left(\frac{\sqrt{2}}{2}; \frac{\sqrt{2}}{2}\right)\), \(M_4 \left(-\frac{\sqrt{3}}{2}; \frac{1}{2}\right)\), \(A (1; 0)\), \(B (-1; 0)\) лежат на единичной полуокружности. Выпишите значения синуса, косинуса и тангенса углов \(AOM_1\), \(AOM_2\), \(AOM_3\), \(AOM_4\), \(AOB\).
1) \( M_1(0; 1): 0^2 + 1^2 = 1 \Rightarrow M_1 \in \text{Окр}(0; 1) \);
\( M_2 \left(\frac{1}{2}; \frac{\sqrt{3}}{2}\right): \left(\frac{1}{2}\right)^2 + \left(\frac{\sqrt{3}}{2}\right)^2 = 1 \Rightarrow \frac{1}{4} + \frac{3}{4} = 1 \Rightarrow M_2 \in \text{Окр}(0; 1) \);
\( M_3 \left(\frac{\sqrt{2}}{2}; \frac{\sqrt{2}}{2}\right): \left(\frac{\sqrt{2}}{2}\right)^2 + \left(\frac{\sqrt{2}}{2}\right)^2 = 1 \Rightarrow \frac{1}{2} + \frac{1}{2} = 1 \Rightarrow M_3 \in \text{Окр}(0; 1) \);
\( M_4 \left(-\frac{\sqrt{3}}{2}; \frac{1}{2}\right): \left(-\frac{\sqrt{3}}{2}\right)^2 + \left(\frac{1}{2}\right)^2 = 1 \Rightarrow \frac{3}{4} + \frac{1}{4} = 1 \Rightarrow M_4 \in \text{Окр}(0; 1) \);
\( A(1; 0): 1^2 + 0^2 = 1 \Rightarrow A \in \text{Окр}(0; 1) \);
\( B(-1; 0): (-1)^2 + 0^2 = 1 \Rightarrow B \in \text{Окр}(0; 1) \);
2) Отобразим условие задачи
\(
\sin \angle AOM_1 = \sin 90^\circ = 1; \quad \cos \angle AOM_1 = 0; \quad \tan \angle AOM_1 \)- не существует;
\(
\sin \angle AOM_2 = \frac{\sqrt{3}}{2}; \quad \cos \angle AOM_2 = \frac{1}{2}; \quad \tan \angle AOM_2 = \frac{\sin \angle AOM_2}{\cos \angle AOM_2} = \)
\(= \sqrt{3};
\)
\(
\sin \angle AOM_3 = \frac{\sqrt{2}}{2}; \quad \cos \angle AOM_3 = \frac{\sqrt{2}}{2}; \quad \tan \angle AOM_3 = \frac{\sin \angle AOM_3}{\cos \angle AOM_3} = 1;
\)
\(
\sin \angle AOM_4 = \frac{1}{2}; \quad \cos \angle AOM_4 = -\frac{\sqrt{3}}{2}; \quad \tan \angle AOM_4 = \frac{\sin \angle AOM_4}{\cos \angle AOM_4} = \)
\(=-\sqrt{3};
\)
\(
\sin \angle AOB = 0; \quad \cos \angle AOB = -1; \quad \tan \angle AOB = \frac{\sin \angle AOB}{\cos \angle AOB} = 0;
\)
Проверим, что точки \( M_1(0; 1) \), \( M_2 \left(\frac{1}{2}; \frac{\sqrt{3}}{2}\right) \), \( M_3 \left(\frac{\sqrt{2}}{2}; \frac{\sqrt{2}}{2}\right) \), \( M_4 \left(-\frac{\sqrt{3}}{2}; \frac{1}{2}\right) \), \( A(1; 0) \), \( B(-1; 0) \) лежат на единичной окружности с центром в начале координат. Для этого проверим, что сумма квадратов координат каждой точки равна 1.
Для точки \( M_1(0; 1) \):
\(
0^2 + 1^2 = 0 + 1 = 1
\)
Следовательно, \( M_1 \) лежит на окружности.
Для точки \( M_2 \left(\frac{1}{2}; \frac{\sqrt{3}}{2}\right) \):
\(
\left(\frac{1}{2}\right)^2 + \left(\frac{\sqrt{3}}{2}\right)^2 = \frac{1}{4} + \frac{3}{4} = 1
\)
Следовательно, \( M_2 \) лежит на окружности.
Для точки \( M_3 \left(\frac{\sqrt{2}}{2}; \frac{\sqrt{2}}{2}\right) \):
\(
\left(\frac{\sqrt{2}}{2}\right)^2 + \left(\frac{\sqrt{2}}{2}\right)^2 = \frac{2}{4} + \frac{2}{4} = 1
\)
Следовательно, \( M_3 \) лежит на окружности.
Для точки \( M_4 \left(-\frac{\sqrt{3}}{2}; \frac{1}{2}\right) \):
\(
\left(-\frac{\sqrt{3}}{2}\right)^2 + \left(\frac{1}{2}\right)^2 = \frac{3}{4} + \frac{1}{4} = 1
\)
Следовательно, \( M_4 \) лежит на окружности.
Для точки \( A(1; 0) \):
\(
1^2 + 0^2 = 1 + 0 = 1
\)
Следовательно, \( A \) лежит на окружности.
Для точки \( B(-1; 0) \):
\(
(-1)^2 + 0^2 = 1 + 0 = 1
\)
Следовательно, \( B \) лежит на окружности.
Теперь найдем синус, косинус и тангенс углов \( \angle AOM_1 \), \( \angle AOM_2 \), \( \angle AOM_3 \), \( \angle AOM_4 \), \( \angle AOB \).
Для угла \( \angle AOM_1 \):
\(
\sin \angle AOM_1 = \sin 90^\circ = 1
\)
\(
\cos \angle AOM_1 = 0
\)
\(
\tan \angle AOM_1 \text{ не существует}
\)
Для угла \( \angle AOM_2 \):
\(
\sin \angle AOM_2 = \frac{\sqrt{3}}{2} \approx 0.866
\)
\(
\cos \angle AOM_2 = \frac{1}{2} = 0.5
\)
\(
\tan \angle AOM_2 = \frac{\sin \angle AOM_2}{\cos \angle AOM_2} = \frac{\sqrt{3}/2}{1/2} = \sqrt{3} \approx 1.732
\)
Для угла \( \angle AOM_3 \):
\(
\sin \angle AOM_3 = \frac{\sqrt{2}}{2} \approx 0.707
\)
\(
\cos \angle AOM_3 = \frac{\sqrt{2}}{2} \approx 0.707
\)
\(
\tan \angle AOM_3 = \frac{\sin \angle AOM_3}{\cos \angle AOM_3} = \frac{\sqrt{2}/2}{\sqrt{2}/2} = 1
\)
Для угла \( \angle AOM_4 \):
\(
\sin \angle AOM_4 = \frac{1}{2} = 0.5
\)
\(
\cos \angle AOM_4 = -\frac{\sqrt{3}}{2} \approx -0.866
\)
\(
\tan \angle AOM_4 = \frac{\sin \angle AOM_4}{\cos \angle AOM_4} = \frac{1/2}{-\sqrt{3}/2} = -\frac{1}{\sqrt{3}} \approx -0.577
\)
Для угла \( \angle AOB \):
\(
\sin \angle AOB = 0
\)
\(
\cos \angle AOB = -1
\)
\(
\tan \angle AOB = \frac{\sin \angle AOB}{\cos \angle AOB} = 0
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!