
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1011 Атанасян — Подробные Ответы
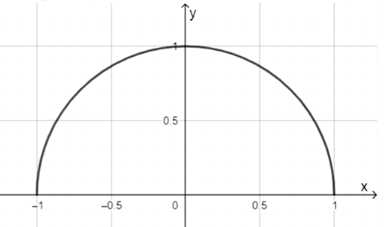
Ответьте на вопросы: а) Может ли абсцисса точки единичной полуокружности иметь значения 0,3; \(\frac{1}{3}\); \(-\frac{1}{3}\); 1, \(\frac{2}{3}\); -2,8? б) Может ли ордината точки единичной полуокружности иметь значения 0,6; \(\frac{1}{7}\); -0,3; 7; 1,002? Ответы обоснуйте.
Для решения задачи, представленной на изображении, необходимо определить возможные значения абсцисс и ординат точек на единичной полуокружности.
а) Абсцисса точек на единичной полуокружности может принимать значения: \(0,3\); \(\frac{1}{3}\); \(-\frac{1}{3}\).
б) Ордината точек на единичной полуокружности может принимать значения: \(0,6\); \(\frac{1}{7}\).
Эти значения соответствуют возможным координатам точек на полуокружности радиуса 1, расположенной в первой и второй четвертях координатной плоскости.
Рассмотрим единичную полуокружность с центром в начале координат и радиусом 1. Уравнение окружности имеет вид: \(x^2 + y^2 = 1\).
а) Найдем возможные значения абсцисс (x):
1. Подставим каждое значение абсциссы в уравнение окружности и найдем соответствующую ординату (y):
— Для \(x = 0,3\):
\(
(0,3)^2 + y^2 = 1 \Rightarrow 0,09 + y^2 = 1 \Rightarrow y^2 = 0,91 \Rightarrow y = \pm \sqrt{0,91}
\)
Приближенные значения: \(y \approx \pm 0,95\).
— Для \(x = \frac{1}{3}\):
\(
\left(\frac{1}{3}\right)^2 + y^2 = 1 \Rightarrow \frac{1}{9} + y^2 = 1 \Rightarrow y^2 = \frac{8}{9} \Rightarrow y = \pm \frac{\sqrt{8}}{3}
\)
Приближенные значения: \(y \approx \pm 0,94\).
— Для \(x = -\frac{1}{3}\):
\(
\left(-\frac{1}{3}\right)^2 + y^2 = 1 \Rightarrow \frac{1}{9} + y^2 = 1 \Rightarrow y^2 = \frac{8}{9} \Rightarrow y = \pm \frac{\sqrt{8}}{3}
\)
Приближенные значения: \(y \approx \pm 0,94\).
б) Найдем возможные значения ординат (y):
1. Подставим каждое значение ординаты в уравнение окружности и найдем соответствующую абсциссу (x):
— Для \(y = 0,6\):
\(
x^2 + (0,6)^2 = 1 \Rightarrow x^2 + 0,36 = 1 \Rightarrow x^2 = 0,64 \Rightarrow x = \pm \sqrt{0,64}
\)
Приближенные значения: \(x \approx \pm 0,8\).
— Для \(y = \frac{1}{7}\):
\(
x^2 + \left(\frac{1}{7}\right)^2 = 1 \Rightarrow x^2 + \frac{1}{49} = 1 \Rightarrow x^2 = \frac{48}{49} \Rightarrow x = \pm \frac{\sqrt{48}}{7}
\)
Приближенные значения: \(x \approx \pm 0,99\).
Таким образом, мы нашли возможные значения абсцисс и ординат, которые соответствуют точкам на единичной полуокружности.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!