ГДЗ по Геометрии 9 класс Номер 1009 Атанасян — Подробные Ответы

Докажите, что медиану \(AA_1\) треугольника \(ABC\) можно вычислить по формуле \(AA_1 = \frac{1}{2} \sqrt{2AC^2 + 2AB^2 — BC^2}\). Используя эту формулу, докажите, что если две медианы треугольника равны, то треугольник равнобедренный.

Для доказательства формулы медианы треугольника \( \Delta ABC \) используем следующее:

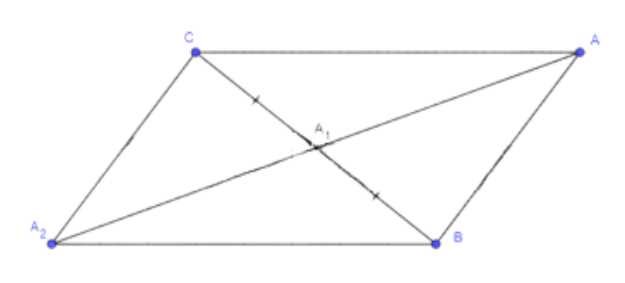
1. Продлим медиану \( AA_1 \) до точки \( A_2 \), чтобы \( AA_1 = A_1A_2 \). Тогда \( CA_1A_2B \) — параллелограмм.
2. По свойству параллелограмма:
\[
(AA_2)^2 + (CB)^2 = (AC)^2 + (AB)^2 + (BA_2)^2 + (CA_2)^2
\]
3. Упростим:
\[
(AA_2)^2 = 2(AC)^2 + 2(AB)^2 — (BC)^2
\]
4. Отсюда медиана:
\[
AA_1 = \frac{1}{2} \sqrt{2(AC)^2 + 2(AB)^2 — (BC)^2}
\]

Для доказательства равенства медиан и равнобедренности:

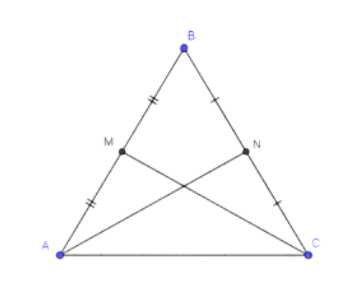
1. Пусть \( AN = CM \). Тогда:
\[
CM = \frac{1}{2} \sqrt{2(BC)^2 + 2(AC)^2 — (AB)^2}
\]
\[
AN = \frac{1}{2} \sqrt{2(AB)^2 + 2(AC)^2 — (BC)^2}
\]
2. Приравниваем:
\[
\frac{1}{2} \sqrt{2(BC)^2 + 2(AC)^2 — (AB)^2} = \frac{1}{2} \sqrt{2(AB)^2 + 2(AC)^2 — (BC)^2}
\]
3. Из этого следует:
\[
2(BC)^2 + 2(AC)^2 — (AB)^2 = 2(AB)^2 + 2(AC)^2 — (BC)^2
\]
4. Упростим:
\[
3(BC)^2 = 3(AB)^2 \Rightarrow BC = AB
\]

Таким образом, треугольник равнобедренный.

Для доказательства формулы медианы треугольника \(\Delta ABC\) и равнобедренности, если две медианы равны, следуем следующим шагам:

1. Дополнительное построение: Продлим медиану \(AA_1\) до точки \(A_2\) так, чтобы \(AA_1 = A_1A_2\). Тогда \(CA_1A_2B\) будет параллелограммом.

2. Используем свойства параллелограмма: В параллелограмме диагонали делятся пополам, и квадрат длины диагонали равен сумме квадратов всех сторон.

3. Запишем уравнение для параллелограмма:
\[
(AA_2)^2 + (CB)^2 = (AC)^2 + (AB)^2 + (BA_2)^2 + (CA_2)^2
\]

4. Упростим уравнение: Поскольку \(BA_2 = AC\) и \(CA_2 = AB\), уравнение становится:
\[
(AA_2)^2 = 2(AC)^2 + 2(AB)^2 — (BC)^2
\]

5. Выразим медиану \(AA_1\):
\[
AA_1 = \frac{1}{2} \sqrt{2(AC)^2 + 2(AB)^2 — (BC)^2}
\]

Теперь докажем, что если две медианы равны, то треугольник равнобедренный:

1. Условие: Пусть \(AN = CM\). Тогда для медиан имеем:
\[
CM = \frac{1}{2} \sqrt{2(BC)^2 + 2(AC)^2 — (AB)^2}
\]
\[
AN = \frac{1}{2} \sqrt{2(AB)^2 + 2(AC)^2 — (BC)^2}
\]

2. Приравниваем медианы:
\[
\frac{1}{2} \sqrt{2(BC)^2 + 2(AC)^2 — (AB)^2} = \frac{1}{2} \sqrt{2(AB)^2 + 2(AC)^2 — (BC)^2}
\]

3. Упростим уравнение:
\[
2(BC)^2 + 2(AC)^2 — (AB)^2 = 2(AB)^2 + 2(AC)^2 — (BC)^2
\]

4. Сокращаем и решаем:
\[
3(BC)^2 = 3(AB)^2
\]
\[
BC = AB
\]

Таким образом, треугольник \(\Delta ABC\) является равнобедренным, что и требовалось доказать.