Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1006 Атанасян — Подробные Ответы
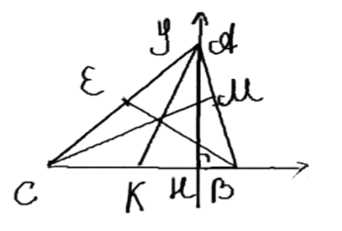
Две стороны треугольника равны 17 см и 28 см, а высота, проведённая к большей из них, равна 15 см. Найдите медианы треугольника.
Решение:
1. Введем систему координат: \( A(0; 0) \), \( B(x; 15) \), \( C(28; 0) \).
2. Найдем координаты точки \( B \) из условия \( AB = 17 \):
\[
\sqrt{x^2 + 15^2} = 17 \Rightarrow x^2 = 289 — 225 \Rightarrow x^2 = 64 \Rightarrow x = \pm 8
\]
Выбираем \( x = 8 \) (так как \( x > 0 \)), значит \( B(8; 15) \).
3. Находим координаты середины отрезков:
— \( A_1 \) — середина \( BC \):
\[
x_1 = \frac{8 + 28}{2} = 18, \quad y_1 = \frac{15 + 0}{2} = 7.5
\]
— \( B_1 \) — середина \( CA \):
\[
x_2 = \frac{0 + 28}{2} = 14, \quad y_2 = \frac{0 + 0}{2} = 0
\]
— \( C_1 \) — середина \( AB \):
\[
x_3 = \frac{0 + 8}{2} = 4, \quad y_3 = \frac{0 + 15}{2} = 7.5
\]
4. Вычисляем длины медиан:
— \( AA_1 \):
\[
AA_1 = \sqrt{(18 — 0)^2 + (7.5 — 0)^2} = 19.5 \, \text{см}
\]
— \( BB_1 \):
\[
BB_1 = \sqrt{(14 — 8)^2 + (0 — 15)^2} = 3\sqrt{29} \, \text{см}
\]
— \( CC_1 \):
\[
CC_1 = \sqrt{(4 — 28)^2 + (7.5 — 0)^2} = \frac{3}{2}\sqrt{281} \, \text{см}
\]
Ответ: \( AA_1 = 19.5 \, \text{см} \), \( BB_1 = 3\sqrt{29} \, \text{см} \), \( CC_1 = \frac{3}{2}\sqrt{281} \, \text{см} \).
Решение задачи о нахождении медиан в треугольнике \(\triangle ABC\) с заданными сторонами и высотой требует введения системы координат и использования формул для вычисления расстояний.
1. Введем систему координат:
— Пусть \( A(0; 0) \), \( C(28; 0) \).
— Точка \( B \) имеет координаты \( (x, 15) \) из условия, что высота \( BH = 15 \).
2. Найдем координаты точки \( B \) из условия, что \( AB = 17 \):
\[
\sqrt{x^2 + 15^2} = 17
\]
\[
x^2 + 225 = 289
\]
\[
x^2 = 64
\]
\[
x = \pm 8
\]
Поскольку \( x > 0 \), выбираем \( x = 8 \). Следовательно, \( B(8; 15) \).
3. Найдем координаты середины отрезков \( BC \), \( CA \), \( AB \):
— Середина \( BC \) — точка \( A_1 \):
\[
x_1 = \frac{8 + 28}{2} = 18
\]
\[
y_1 = \frac{15 + 0}{2} = 7.5
\]
— Середина \( CA \) — точка \( B_1 \):
\[
x_2 = \frac{0 + 28}{2} = 14
\]
\[
y_2 = \frac{0 + 0}{2} = 0
\]
— Середина \( AB \) — точка \( C_1 \):
\[
x_3 = \frac{0 + 8}{2} = 4
\]
\[
y_3 = \frac{0 + 15}{2} = 7.5
\]
4. Вычислим длины медиан:
— Медиана \( AA_1 \):
\[
AA_1 = \sqrt{(18 — 0)^2 + (7.5 — 0)^2}
\]
\[
AA_1 = \sqrt{18^2 + 7.5^2} = \sqrt{324 + 56.25} = \sqrt{380.25} \approx 19.5 \, \text{см}
\]
— Медиана \( BB_1 \):
\[
BB_1 = \sqrt{(14 — 8)^2 + (0 — 15)^2}
\]
\[
BB_1 = \sqrt{6^2 + 15^2} = \sqrt{36 + 225} = \sqrt{261} = 3\sqrt{29} \, \text{см}
\]
— Медиана \( CC_1 \):
\[
CC_1 = \sqrt{(4 — 28)^2 + (7.5 — 0)^2}
\]
\[
CC_1 = \sqrt{(-24)^2 + 7.5^2} = \sqrt{576 + 56.25} = \sqrt{632.25} = \frac{3}{2}\sqrt{281} \, \text{см}
\]
Ответ: \( AA_1 \approx 19.5 \, \text{см} \), \( BB_1 = 3\sqrt{29} \, \text{см} \), \( CC_1 = \frac{3}{2}\sqrt{281} \, \text{см} \).
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.