ГДЗ по Геометрии 7 класс Номер 94 Атанасян — Подробные Ответы

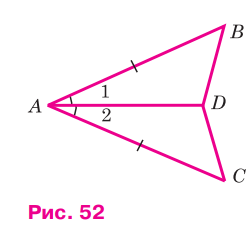
На рисунке 52 AB = АС, ∠1 = ∠2. а) Докажите, что треугольники ABD и ACD равны; б) найдите BD и AB, если АС = 15 см, DC = 5 см.

Дано: \(AB = AC\), \(\angle 1 = \angle 2\), \(AC = 15\) см, \(DC = 5\) см.

а) В треугольниках \(ABD\) и \(ACD\): \(AB = AC\) (по условию), \(AD\) — общая сторона, \(\angle 1 = \angle 2\) (по условию). По первому признаку равенства треугольников (две стороны и угол между ними) треугольники \(ABD\) и \(ACD\) равны.

б) Так как треугольники равны, \(BD = DC = 5\) см. Тогда \(BC = BD + DC = 5 + 5 = 10\) см. В равнобедренном треугольнике \(ABC\) медиана \(AD\) делит основание \(BC\) пополам. Найдём \(AD\) по формуле высоты:

\(AD = \sqrt{AB^2 — \left(\frac{BC}{2}\right)^2} = \sqrt{15^2 — \left(\frac{10}{2}\right)^2} = \sqrt{225 — 25} = \sqrt{200} = 10\sqrt{2}\) см.

Проверим \(AB\) по теореме Пифагора:

\(AB = \sqrt{BD^2 + AD^2} = \sqrt{5^2 + (10\sqrt{2})^2} = \sqrt{25 + 200} = \sqrt{225} = 15\) см.

Ответ: а) треугольники \(ABD\) и \(ACD\) равны; б) \(BD = 5\) см, \(AB = 15\) см.

Дано, что \(AB = AC\) и углы при вершине \(A\), обозначенные как \(\angle 1\) и \(\angle 2\), равны: \(\angle 1 = \angle 2\). Это означает, что треугольники \(ABD\) и \(ACD\) имеют по условию равные по длине стороны \(AB\) и \(AC\), а также равные углы между сторонами \(AB\) и \(AD\), и \(AC\) и \(AD\) соответственно. Общая сторона у этих треугольников — \(AD\). По первому признаку равенства треугольников, который гласит, что если две стороны и угол между ними одного треугольника равны соответствующим двум сторонам и углу другого треугольника, то такие треугольники равны, можно утверждать, что \( \triangle ABD = \triangle ACD \).

Поскольку треугольники равны, то и соответствующие стороны у них равны. Следовательно, \(BD = DC\). По условию \(DC = 5\) см, значит \(BD = 5\) см. Теперь рассмотрим треугольник \(ABC\). Поскольку \(AB = AC\), треугольник \(ABC\) равнобедренный с основанием \(BC\). Длина основания \(BC\) равна сумме отрезков \(BD\) и \(DC\), то есть \(BC = BD + DC = 5 + 5 = 10\) см. Медиана \(AD\), проведённая к основанию \(BC\), делит его пополам, значит \(BD = DC = \frac{BC}{2} = 5\) см.

Для нахождения длины медианы \(AD\) используем формулу высоты в равнобедренном треугольнике: \(AD = \sqrt{AB^2 — \left(\frac{BC}{2}\right)^2}\). Подставляем известные значения: \(AD = \sqrt{15^2 — 5^2} = \sqrt{225 — 25} = \sqrt{200} = 10\sqrt{2}\) см. Проверим теперь длину стороны \(AB\) с помощью теоремы Пифагора в треугольнике \(ABD\), где \(AB\) — гипотенуза, а \(BD\) и \(AD\) — катеты. Получаем \(AB = \sqrt{BD^2 + AD^2} = \sqrt{5^2 + (10\sqrt{2})^2} = \sqrt{25 + 200} = \sqrt{225} = 15\) см, что совпадает с условием.

Таким образом, доказано, что треугольники \(ABD\) и \(ACD\) равны по первому признаку равенства треугольников. Из равенства треугольников следует, что \(BD = DC = 5\) см. В равнобедренном треугольнике \(ABC\) медиана \(AD\) делит основание \(BC\) на равные части, и длина \(AB\) равна 15 см, что соответствует условию задачи. Итоговый ответ: \(BD = 5\) см, \(AB = 15\) см, треугольники \(ABD\) и \(ACD\) равны.