ГДЗ по Геометрии 7 класс Номер 86 Атанасян — Подробные Ответы

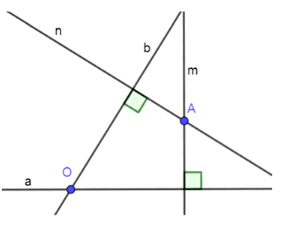
Даны две пересекающиеся прямые а и b и точка А, не лежащая на этих прямых. Через точку А проведены прямые m и n так, что m ⊥ a, n ⊥ b. Докажите, что прямые m и n не совпадают.

Предположим, что прямые m и n совпадают. Это означает, что они лежат на одной прямой k. В таком случае, прямая k будет одновременно перпендикулярна прямой a и прямой b, так как m ⊥ a и n ⊥ b. Однако, одна прямая не может быть перпендикулярна двум различным пересекающимся прямым, так как это возможно только в случае, если прямые a и b параллельны. Но по условию задачи прямые a и b не являются параллельными. Таким образом, наше предположение о совпадении прямых m и n оказалось неверным. Следовательно, прямые m и n не совпадают.

Рассмотрим задачу. Даны две пересекающиеся прямые a и b и точка A, не лежащая на этих прямых. Через точку A проведены прямые m и n так, что m перпендикулярна прямой a, а n перпендикулярна прямой b. Необходимо доказать, что прямые m и n не совпадают.

1. Предположим, что прямые m и n совпадают. Это означает, что они лежат на одной прямой k, которая проходит через точку A.

2. Так как m перпендикулярна прямой a, то прямая k также будет перпендикулярна прямой a.

3. Аналогично, так как n перпендикулярна прямой b, то прямая k также будет перпендикулярна прямой b.

4. Таким образом, получается, что одна и та же прямая k перпендикулярна двум различным пересекающимся прямым a и b.

5. Однако это невозможно. Прямая может быть перпендикулярна двум различным прямым только в том случае, если эти прямые параллельны. Но по условию задачи прямые a и b пересекаются, а значит, они не параллельны.

6. Полученное противоречие указывает на то, что наше предположение о том, что прямые m и n совпадают, неверно.

7. Следовательно, прямые m и n не совпадают.

Таким образом, доказательство завершено. Прямые m и n действительно не совпадают.