ГДЗ по Геометрии 7 класс Номер 83 Атанасян — Подробные Ответы

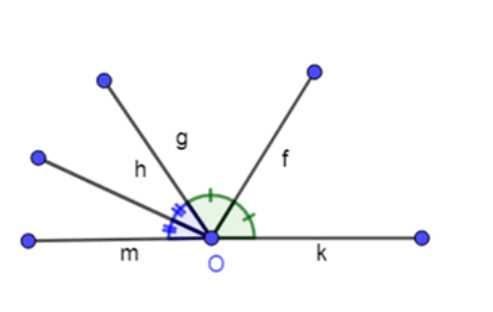
Найдите угол, образованный биссектрисами двух смежных углов.

Дано: \(h\) — биссектриса угла \( \angle mg\), \(f\) — биссектриса угла \( \angle gk\).

По свойству смежных углов:
\( \angle mg + \angle gk = 180^\circ \).

Угол \( \angle hf \) раскладывается как сумма:
\( \angle hf = \angle hg + \angle gf \).

Так как \(h\) и \(f\) — биссектрисы углов \( \angle mg \) и \( \angle gk \), то:
\( \angle hg = \frac{\angle mg}{2} \),
\( \angle gf = \frac{\angle gk}{2} \).

Следовательно,
\( \angle hf = \frac{\angle mg}{2} + \frac{\angle gk}{2} = \frac{\angle mg + \angle gk}{2} = \frac{180^\circ}{2} = 90^\circ \).

Ответ: \( \angle hf = 90^\circ \).

1) Отобразим условие задачи:
Дано, что \(h\) — биссектриса угла \( \angle mg\), а \(f\) — биссектриса угла \( \angle gk\). Нужно найти угол \( \angle hf\).

2) Рассмотрим выражение для угла \( \angle hf\). По построению и свойствам углов:
\( \angle hf = \angle hg + \angle gf\).

3) Известно, что углы \( \angle mg\) и \( \angle gk\) являются смежными, следовательно:
\( \angle mg + \angle gk = 180^\circ\).

4) Сложим углы вокруг точки \(O\):
\( \angle mh + \angle hg + \angle gf + \angle fk = 180^\circ\).

5) Поскольку \(h\) и \(f\) — биссектрисы углов \( \angle mg\) и \( \angle gk\), то:
\( \angle hg = \angle mh = \frac{\angle mg}{2}\),
\( \angle gf = \angle fk = \frac{\angle gk}{2}\).

6) Подставим эти значения в сумму углов:
\( \angle hg + \angle gf = \frac{\angle mg}{2} + \frac{\angle gk}{2} = \frac{\angle mg + \angle gk}{2}\).

7) Используем равенство смежных углов:
\( \frac{\angle mg + \angle gk}{2} = \frac{180^\circ}{2} = 90^\circ\).

8) Следовательно,
\( \angle hf = 90^\circ\).

Ответ: \( \angle hf = 90^\circ\).