ГДЗ по Геометрии 7 класс Номер 75 Атанасян — Подробные Ответы

Три точки K, L, M лежат на одной прямой, KL = 6 см, LM = 10 см. Каким может быть расстояние KM? Для каждого из возможных случаев сделайте чертёж.

Решение:

1. Точки K, L и M лежат на одной прямой. Расстояние между K и M зависит от их взаимного расположения.

2. Возможны два случая:
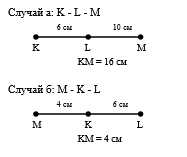
а) Точки расположены в порядке K — L — M. Тогда KM = KL + LM = 6 + 10 = 16 см.
б) Точки расположены в порядке M — K — L. Тогда KM = LM — KL = 10 — 6 = 4 см.

Чертежи для каждого случая:

Рассмотрим задачу о нахождении расстояния между точками K и M, если точки K, L и M лежат на одной прямой. Даны следующие данные:

• Расстояние между точками K и L равно 6 см.
• Расстояние между точками L и M равно 10 см.

Анализ задачи:
Так как точки K, L и M лежат на одной прямой, возможны два варианта их взаимного расположения:

1. Точки расположены в порядке K — L — M.
2. Точки расположены в порядке M — K — L.

От выбора порядка расположения точек зависит итоговое расстояние между K и M.

Решение для первого случая: K — L — M
Если точки расположены в порядке K — L — M, то расстояние между K и M равно сумме расстояний KL и LM, так как они складываются вдоль одной прямой:
KM = KL + LM.
Подставляем значения:
KM = 6 + 10 = 16 см.

Решение для второго случая: M — K — L
Если точки расположены в порядке M — K — L, то расстояние между K и M равно разности расстояний LM и KL, так как точка K находится между M и L:
KM = LM — KL.
Подставляем значения:
KM = 10 — 6 = 4 см.

Вывод:
Таким образом, в зависимости от взаимного расположения точек K, L и M, расстояние между K и M может быть равно:

1. 16 см, если точки расположены в порядке K — L — M.
2. 4 см, если точки расположены в порядке M — K — L.

Для наглядности представим два возможных расположения точек.