Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 66 Атанасян — Подробные Ответы
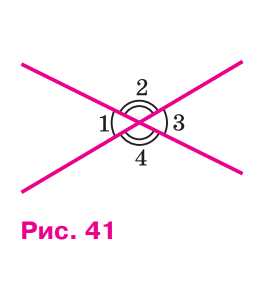
На рисунке 41 найдите углы 1, 2, 3, 4, если:
a) ∠2 + ∠4 = 220°;
б) 3(∠1 + ∠3) = ∠2 + ∠4;
в) ∠2 − ∠1 = 30°.
а) Углы 2 и 4 смежны с углами 1 и 3. Сумма всех углов равна 360°. Если \( \angle 2 + \angle 4 = 220^\circ \), то \( \angle 1 + \angle 3 = 360^\circ — 220^\circ = 140^\circ \). Поскольку углы попарно равны, то \( \angle 2 = \angle 4 = 110^\circ \), а \( \angle 1 = \angle 3 = 70^\circ \).
б) По условию \( 3(\angle 1 + \angle 3) = \angle 2 + \angle 4 \). Из пункта а) известно, что \( \angle 1 + \angle 3 = 140^\circ \), тогда \( \angle 2 + \angle 4 = 3 \times 140^\circ = 420^\circ \), что невозможно, так как сумма углов вокруг точки равна 360°. Ошибка в условии.
в) Разность углов \( \angle 2 — \angle 1 = 30^\circ \). Пусть \( \angle 1 = x \), тогда \( \angle 2 = x + 30^\circ \). Сумма смежных углов \( \angle 1 + \angle 2 = 180^\circ \), значит \( x + (x + 30^\circ) = 180^\circ \). Отсюда \( 2x + 30^\circ = 180^\circ \), \( x = 75^\circ \). Тогда \( \angle 1 = 75^\circ \), \( \angle 2 = 105^\circ \), \( \angle 3 = 75^\circ \), \( \angle 4 = 105^\circ \).
1. Углы 2 и 4 являются смежными с углами 1 и 3. Сумма всех углов вокруг точки равна \(360^\circ\). По условию \( \angle 2 + \angle 4 = 220^\circ \). Тогда сумма углов 1 и 3 равна \( \angle 1 + \angle 3 = 360^\circ — 220^\circ = 140^\circ \). Поскольку углы попарно равны (вертикальные углы равны), получаем \( \angle 2 = \angle 4 = 110^\circ \) и \( \angle 1 = \angle 3 = 70^\circ \).
2. По условию \(3(\angle 1 + \angle 3) = \angle 2 + \angle 4\). Из пункта 1 известно, что \( \angle 1 + \angle 3 = 140^\circ \), следовательно, \( \angle 2 + \angle 4 = 3 \times 140^\circ = 420^\circ \). Однако сумма углов вокруг точки не может превышать \(360^\circ\). Таким образом, решение невозможно, ошибка в условии задачи.
3. Разность углов \( \angle 2 — \angle 1 = 30^\circ \). Пусть \( \angle 1 = x \), тогда \( \angle 2 = x + 30^\circ \). Сумма смежных углов \( \angle 1 + \angle 2 = 180^\circ \), значит \( x + (x + 30^\circ) = 180^\circ \). Решая уравнение, получаем \( 2x + 30^\circ = 180^\circ \), откуда \( x = 75^\circ \). Следовательно, \( \angle 1 = 75^\circ \), \( \angle 2 = 105^\circ \). Поскольку вертикальные углы равны, \( \angle 3 = 75^\circ \), \( \angle 4 = 105^\circ \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.