
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 63 Атанасян — Подробные Ответы
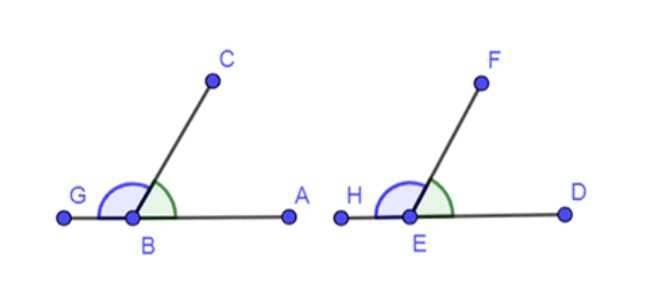
Даны два равных угла. Равны ли смежные с ними углы?
Дано: \(\angle ABC = \angle DEF\).
Сумма смежных углов равна 180°, значит:
\(\angle CBG = 180^\circ — \angle ABC\),
\(\angle HEF = 180^\circ — \angle FED\).
Так как \(\angle ABC = \angle DEF\), то
\(\angle HEF = 180^\circ — \angle ABC\).
Следовательно,
\(\angle HEF = \angle CBG\).
Ответ: смежные углы будут равны.
1) Отобразим условие задачи.
Даны два угла: \(\angle ABC\) и \(\angle DEF\), при этом известно, что \(\angle ABC = \angle DEF\).
Необходимо доказать, что смежные с ними углы \(\angle CBG\) и \(\angle HEF\) равны.
2) Решение.
Сумма смежных углов равна \(180^\circ\), следовательно:
\(\angle CBG = 180^\circ — \angle ABC\).
Аналогично для второго угла:
\(\angle HEF = 180^\circ — \angle FED\).
3) Так как углы \(\angle ABC\) и \(\angle DEF\) равны, то угол \(\angle HEF\) можно выразить как:
\(\angle HEF = 180^\circ — \angle ABC\).
4) Из этого следует, что:
\(\angle HEF = \angle CBG\).
Что и требовалось доказать.
Ответ: смежные углы будут равны.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!