ГДЗ по Геометрии 7 класс Номер 57 Атанасян — Подробные Ответы

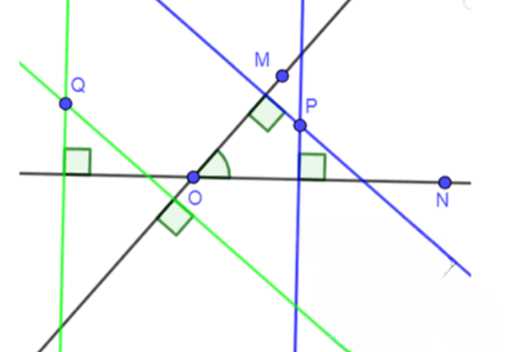
Начертите неразвёрнутый угол MON и отметьте точку P внутри угла и точку Q вне его. С помощью чертёжного угольника и линейки через точки P и Q проведите прямые, перпендикулярные к прямым OM и ON.

Построим угол \(MON\), обозначим точки \(P\) и \(Q\).

Проведём перпендикулярные прямые к сторонам угла: к \(MO\) через точку \(P\) и к \(ON\) через точку \(Q\). Эти прямые пересекутся с продолжениями сторон угла, образуя прямоугольные треугольники.

Таким образом, построены перпендикулярные прямые к сторонам угла \(MON\) через заданные точки \(P\) и \(Q\), что соответствует условию задачи.

1) Построим угол \(MON\). Для этого проведём две лучевые линии, исходящие из точки \(O\): одну через точку \(M\), другую через точку \(N\). Угол \(MON\) образован этими двумя лучами.

Обозначим на плоскости точки \(P\) и \(Q\), расположенные вне угла \(MON\), как показано на рисунке.

2) Проведём перпендикулярные прямые к сторонам угла \(MON\).

К стороне \(MO\) проведём прямую, проходящую через точку \(P\), такую что она перпендикулярна \(MO\). Это означает, что угол между прямой через \(P\) и \(MO\) равен \(90^{\circ}\).

Аналогично, к стороне \(ON\) проведём прямую, проходящую через точку \(Q\), перпендикулярную \(ON\). Угол между этой прямой и \(ON\) также равен \(90^{\circ}\).

В результате мы получили две перпендикулярные прямые, каждая из которых проходит через заданные точки \(P\) и \(Q\) соответственно и перпендикулярна одной из сторон угла \(MON\).

Таким образом, построение выполнено согласно условию: есть угол \(MON\) с точками \(P\) и \(Q\), а также перпендикулярные прямые к сторонам угла, проходящие через эти точки.