ГДЗ по Геометрии 7 класс Номер 54 Атанасян — Подробные Ответы

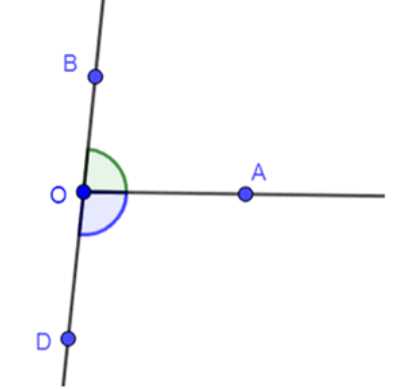
Начертите острый угол АОВ и на продолжении луча ОВ отметьте точку D. Сравните углы АОВ и AOD.

• Начертим острый угол AOB. Это угол, значение которого меньше 90 градусов. Для удобства обозначим вершину угла буквой O, а лучи OA и OB исходят из этой точки.
• Продлим луч OB за точку B и отметим на нем точку D. Теперь у нас есть луч OD, который является продолжением луча OB.
• Рассмотрим угол AOD. Этот угол состоит из двух частей:
  • Угла AOB
  • Развернутого угла DOB, который равен 180 градусам (так как OD — продолжение OB).
• Угол AOD можно выразить как сумму углов: угол AOD = угол AOB + угол DOB.
• Поскольку угол DOB равен 180 градусам, а угол AOB меньше 90 градусов (так как он острый), то угол AOD всегда больше 180 градусов.
• Таким образом, угол AOD является тупым (его величина больше 90 градусов, но меньше 360 градусов).

Вывод: угол AOD всегда больше угла AOB.

Начертим острый угол АОВ. Острый угол — это угол, величина которого строго меньше 90 градусов. Для удобства обозначим вершину угла буквой О, а лучи, исходящие из этой точки, — ОА и ОВ. Таким образом, угол АОВ образован двумя лучами, исходящими из точки О, и его величина находится в интервале \(0^\circ < \angle AOB < 90^\circ\). Это важно, потому что острый угол всегда меньше прямого, и мы будем использовать это свойство для сравнения с другим углом.

Теперь продлим луч ОВ за точку В и отметим на этом продолжении точку D. Получаем новый луч OD, который является прямым продолжением луча ОВ. Поскольку точка D лежит на продолжении луча ОВ, луч OD можно рассматривать как тот же луч ОВ, но выходящий за пределы точки В. Таким образом, луч OD — это продолжение луча ОВ, и они лежат на одной прямой линии, образуя развернутый угол при вершине О.

Рассмотрим угол AOD, образованный лучами ОА и OD. Этот угол можно представить как сумму двух углов: угла АОВ и угла ДОB. Угол ДОB — это развернутый угол, так как луч OD является продолжением луча ОВ, и его величина равна \(180^\circ\). Следовательно, угол AOD можно записать как сумму углов:
\[
\angle AOD = \angle AOB + \angle DOB = \angle AOB + 180^\circ
\]
Поскольку угол АОВ острый, его величина меньше 90 градусов, то есть \(\angle AOB < 90^\circ\). Подставляя это в формулу, получаем:
\[
\angle AOD = \angle AOB + 180^\circ > 180^\circ
\]
Это значит, что угол AOD всегда больше 180 градусов, то есть он является тупым, так как тупой угол — это угол, величина которого больше 90 градусов, но меньше 360 градусов. При этом угол AOD не может быть равен или меньше угла АОВ, так как он включает в себя угол АОВ и дополнительный развернутый угол.

Таким образом, мы видим, что угол AOD всегда больше угла АОВ. Это происходит потому, что угол AOD состоит из суммы острого угла АОВ и развернутого угла DOB, равного 180 градусам. Следовательно, если острый угол АОВ — это угол меньше 90 градусов, то угол AOD будет больше 180 градусов и обязательно больше угла АОВ. Это наглядно демонстрирует, как продолжение луча ОВ за точку В влияет на величину угла, делая угол AOD значительно больше угла АОВ.