ГДЗ Атанасян 7 Класс по Геометрии Бутузов Учебник 📕 Кадомцев- Все Части

Геометрия

7 класс учебник Атанасян

7 класс

Тип

ГДЗ, Решебник.

Автор

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.

Год

2018-2024

Издательство

Просвещение

Описание

Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.

ГДЗ по Геометрии 7 класс Номер 51 Атанасян — Подробные Ответы

Задача

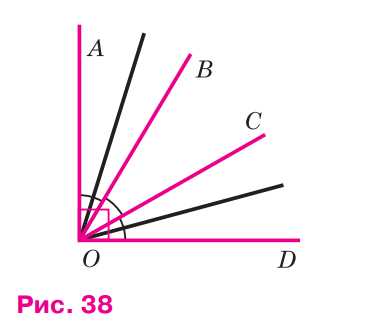
На рисунке 38 угол AOD — прямой, ∠AOB = ∠BOC = ∠COD. Найдите угол, образованный биссектрисами углов AOB и COD.

Краткий ответ:

Угол AOD равен 90° и делится на три равных угла: AOB, BOC и COD, каждый из которых равен 30°. Биссектрисы углов AOB и COD делят их пополам, поэтому каждая половина равна 15°. Угол между биссектрисами равен сумме половины угла AOB, угла BOC и половины угла COD: 15° + 30° + 15° = 60°. Ответ: 60°.

Подробный ответ:

Дано: угол AOD прямой, то есть равен 90°. Углы AOB, BOC и COD равны. Требуется найти угол между биссектрисами углов AOB и COD.

Угол AOD равен 90°, и он делится на три равных угла: AOB, BOC и COD. Каждый из этих углов равен 90° ÷ 3 = 30°.
Биссектриса угла AOB делит его на два равных угла. Следовательно, каждый из этих углов равен 30° ÷ 2 = 15°.
Аналогично, биссектриса угла COD делит его на два равных угла. Каждый из этих углов также равен 30° ÷ 2 = 15°.
Рассмотрим угол между биссектрисами углов AOB и COD. Этот угол состоит из трех частей:
- половины угла AOB, то есть 15°;
- угла BOC, который равен 30°;
- половины угла COD, то есть 15°.
Суммируем все части: угол между биссектрисами = 15° + 30° + 15° = 60°.

Ответ: угол между биссектрисами углов AOB и COD равен 60°.

Оцени решение