ГДЗ по Геометрии 7-9 класс Номер 4 Атанасян — Подробные Ответы

Отметьте точки

A, B, C, D так, чтобы точки A, B, $C$ лежали на одной прямой, а точка D не лежала на ней. Через каждые две точки проведите прямую. Сколько получилось прямых?

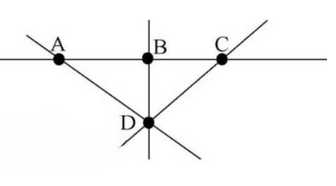
Даны точки A, B, C на одной прямой и точка D вне этой прямой. Нужно провести прямые через каждые две точки.

Всего точек 4. Количество прямых, которые можно провести через любые две точки, равно числу сочетаний из 4 по 2:

\( C_4^2 = \frac{4!}{2! \cdot (4-2)!} = \frac{4 \cdot 3}{2 \cdot 1} = 6 \)

Но так как точки A, B, C лежат на одной прямой, то через них можно провести только одну прямую (не три).

Прямые, которые получаются:

1) Прямая через A, B, C (одна общая)
2) Прямая через A и D
3) Прямая через B и D
4) Прямая через C и D

Итого 4 прямых.

Ответ: 4 прямых.

1. Даны четыре точки: A, B, C и D. Точки A, B, C лежат на одной прямой, а точка D не лежит на этой прямой.

2. Нужно найти количество прямых, которые можно провести через каждую пару точек.

3. Всего точек 4. Количество пар точек равно числу сочетаний из 4 по 2:

\( C_4^2 = \frac{4!}{2! \cdot (4-2)!} = \frac{4 \cdot 3}{2 \cdot 1} = 6 \)

4. Однако, поскольку точки A, B, C лежат на одной прямой, то через них можно провести только одну прямую, а не три.

5. Рассмотрим все возможные пары точек и прямые, которые через них проходят:

— Пара (A, B), (B, C), (A, C) — это одна и та же прямая, обозначим её как прямая ABC.

— Пара (A, D) — прямая AD.

— Пара (B, D) — прямая BD.

— Пара (C, D) — прямая CD.

6. Таким образом, всего получилось 4 прямые:

1) ABC

2) AD

3) BD

4) CD

7. Следовательно, общее количество прямых, проведённых через каждую пару точек, равно 4.