
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 361 Атанасян — Подробные Ответы
Постройте треугольник по периметру и двум углам.
Для построения треугольника ABC с заданным периметром P нужно: построить произвольный треугольник A₁B₁C₁, измерить его стороны.
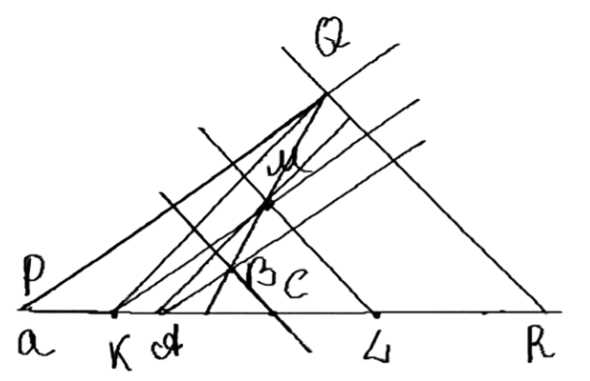
Для построения треугольника ABC с заданным периметром P выполняются следующие шаги:
1. Сначала строим произвольный треугольник A₁B₁C₁. Это можно сделать любым удобным способом, например, выбрав произвольные длины сторон и углы, которые удовлетворяют условиям существования треугольника.
2. Затем строим угол M. На одной из его сторон откладываем отрезок MP, равный заданному периметру P. Точка P будет концом этого отрезка.
3. На второй стороне угла M откладываем три отрезка, равные сторонам треугольника A₁B₁C₁. Сначала откладываем отрезок, равный длине стороны AC₁, затем отрезок, равный длине стороны AB₁, и, наконец, отрезок, равный длине стороны C₁B₁. Конец последнего отрезка обозначаем точкой P₁.
4. Соединяем точки P и P₁ прямой линией. Эта линия называется PP₁. Через точки, лежащие на отрезке MP₁, проводим прямые, которые параллельны линии PP₁. Эти прямые пересекают вторую сторону угла M в точках C’ и B’.
5. Проверяем пропорциональность отрезков. Удостоверяемся, что отрезок MC’ равен длине стороны AC треугольника ABC, отрезок C’B’ равен длине стороны AB, а отрезок BP равен длине стороны BC. Это выполняется благодаря тому, что отрезки на второй стороне угла M пропорциональны сторонам треугольника A₁B₁C₁.
6. На стороне AC₁ откладываем отрезок AC, равный длине отрезка MC’. На стороне AB₁ откладываем отрезок AB, равный длине отрезка C’B’. Соединяем точки A, B и C, завершая построение треугольника ABC.
Таким образом, построение завершается, и треугольник ABC с заданным периметром P построен.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!