
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 360 Атанасян — Подробные Ответы
Постройте треугольник по периметру, одному из углов и высоте, проведённой из вершины другого угла.
Для построения треугольника ABC с высотой h и периметром P выполняем следующие шаги.
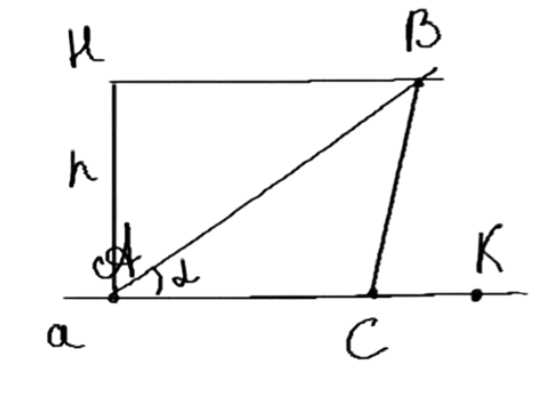
От любой точки A проводим горизонтальный отрезок AP длиной P. Восстанавливаем перпендикуляр из точки A и откладываем на нем высоту h, обозначив верхнюю точку как H. Из точки H проводим горизонтальный отрезок, пересекающий AP в точке B. Находим точку C, чтобы сумма сторон AB, BC и AC равнялась P. Соединяем точки A, B и C, завершая построение.
Для построения треугольника ABC с заданными параметрами (высота h, периметр P) выполним следующие шаги:
1. На стороне угла с вершиной в точке A отложим отрезок AP, равный периметру треугольника. Это означает, что длина отрезка AP равна P. Таким образом, AP = P.
2. В точке A восстановим перпендикуляр к отрезку AP. На этом перпендикуляре отложим отрезок AH, равный высоте треугольника. Таким образом, AH = h.
3. В точке H восстановим перпендикуляр к отрезку AH. Этот перпендикуляр пересекает вторую сторону угла, образованного в точке A. Точку пересечения обозначим как B.
4. На отрезке AP отложим отрезок PK, равный длине стороны AB. Таким образом, PK = AB. Для этого измеряем длину отрезка AB (которая будет определяться в процессе построения) и переносим ее на отрезок AP от точки P.
5. Поскольку периметр треугольника P равен сумме длин сторон AB, BC и AC, то отрезок AK будет равен сумме длин сторон AC и BC. То есть, AK = AC + BC.
6. Соединим точки B и K прямой линией. Затем построим серединный перпендикуляр к отрезку BK. Этот перпендикуляр пересечет отрезок AK в некоторой точке. Точку пересечения обозначим как C.
7. Проверяем, что BC равно CK. Это условие выполняется, так как серединный перпендикуляр гарантирует равенство отрезков BC и CK. Таким образом, точка C расположена корректно.
8. Соединяем точки A, B и C, чтобы завершить построение треугольника ABC.
9. Проверяем построение: измеряем стороны AB, BC и AC, а также высоту AH. Убедимся, что периметр треугольника равен P, а высота AH равна h.
10. Построение завершено. Треугольник ABC с заданными параметрами построен.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!