
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 359 Атанасян — Подробные Ответы
Дана окружность с центром О и точка А вне её. Проведите через точку А прямую, пересекающую окружность в точках В и С таких, что AB = ВС.
Для построения прямой, проходящей через точку A и пересекающей окружность в точках B и C так, чтобы AB = BC, выполняем следующее.
Для построения прямой, проходящей через точку A и пересекающей окружность в точках B и C так, чтобы AB = BC, выполняем следующие шаги:
1. Строим окружность с центром в точке A и радиусом, равным удвоенному радиусу исходной окружности. Обозначим эту окружность как (A; 2R). Это необходимо для того, чтобы задать геометрическое место точек, которые будут использоваться в дальнейшем построении.
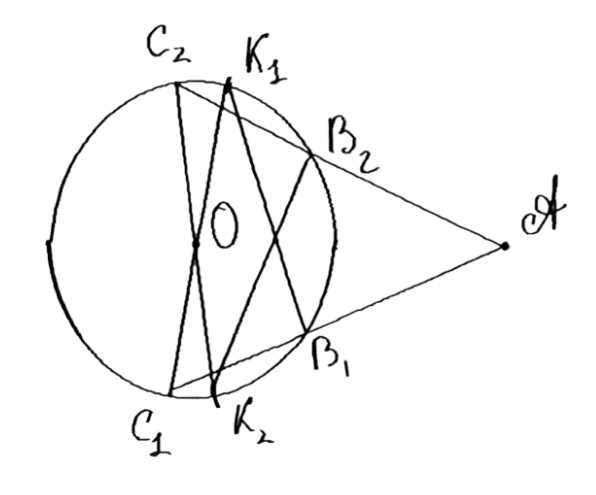
2. Находим точки пересечения окружности (A; 2R) с исходной окружностью (O; R). Эти точки обозначаем как K1 и K2. Они будут ключевыми для дальнейших построений, так как определяют направления лучей.
3. Проводим лучи из точки K1 через центр исходной окружности O и из точки K2 через O. Лучи пересекают исходную окружность (O; R) в точках C1 и C2 соответственно. Эти точки являются промежуточными для построения искомых прямых.
4. Соединяем точку A с точками C1 и C2. Полученные прямые AC1 и AC2 являются искомыми прямыми, которые пересекают окружность (O; R) в точках B1 и B2. Эти точки будут проверяться на выполнение условия задачи.
5. Определяем точки пересечения прямых AC1 и AC2 с исходной окружностью (O; R). Эти точки обозначаем как B1 и B2. Теперь у нас есть все необходимые элементы для проверки равенства отрезков.
6. Рассмотрим треугольники AC1K1 и AC2K2. Они являются равнобедренными, так как радиусы окружности (A; 2R) равны: C1K1 = C2K2 = AK1 = AK2 = 2R. Это следует из построения окружности с центром в точке A и радиусом 2R.
7. Углы K1B1C1 и K2B2C2 являются вписанными, так как они опираются на диаметр окружности (O; R). Это значит, что отрезки K1B1 и K2B2 являются высотами треугольников AC1K1 и AC2K2. Высоты в равнобедренных треугольниках делят основание пополам.
8. Из равенства высот и свойств вписанных углов следует, что отрезки C1B1 и C2B2 равны. Также равны отрезки B1A и B2A. Таким образом, точки B1 и B2 делят отрезки AC1 и AC2 на равные части, что доказывает, что AB = BC.
9. Проверяем построение. Все шаги соответствуют условиям задачи, а равенство отрезков подтверждено свойствами равнобедренных треугольников и вписанных углов.
10. Построение завершено. Прямые AC1 и AC2 являются искомыми, а точки B1 и B2 делят эти прямые так, что AB = BC.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!