Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
Основные особенности учебника:
- Структурированность материала:
- Учебник разделен на логические главы, каждая из которых охватывает определенную тему геометрии, что позволяет легко ориентироваться в материале.
- Доступность изложения:
- Язык и стиль написания адаптированы для школьников, что делает сложные концепции более понятными и доступными.
- Многообразие задач:
- В учебнике представлено множество задач различной сложности, что позволяет каждому ученику найти подходящие для себя упражнения и развивать свои навыки.
- Иллюстрации и схемы:
- Наглядные иллюстрации и схемы помогают лучше усвоить материал и визуализировать геометрические фигуры и их свойства.
- Практические примеры:
- Учебник включает практические примеры из реальной жизни, что делает изучение геометрии более увлекательным и актуальным.
- Поддержка для учителей:
- Включены методические рекомендации, которые помогут преподавателям эффективно использовать материал на уроках.
Заключение
Учебник Атанасяна по геометрии — это отличный инструмент для изучения предмета, который сочетает в себе доступность, разнообразие и практическую направленность. Он подходит как для самостоятельного изучения, так и для использования в классе, что делает его незаменимым помощником в образовательном процессе.
ГДЗ по Геометрии 7 класс Номер 358 Атанасян — Подробные Ответы
Даны три попарно пересекающиеся прямые, не проходящие через одну точку. Постройте точку, равноудалённую от этих прямых. Сколько решений имеет задача?
Для построения точки, равноудаленной от прямых a, b и c, сначала определяем точки пересечения прямых a и b, b и c, обозначив их как A и B.
Строим биссектрисы углов при пересечении прямых a и b в точке A и b и c в точке B. Находим точки пересечения этих биссектрис, обозначив их как M1, M2, M3 и M4. Проверяем, что каждая из этих точек равноудалена от всех трех прямых. Таким образом, задача имеет четыре решения: точки M1, M2, M3 и M4.
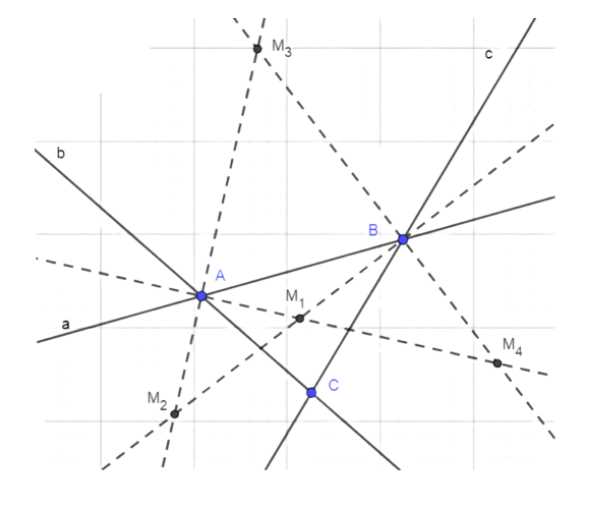
Для построения точки, равноудаленной от трех заданных прямых a, b и c, выполняем следующие шаги:
1. Определяем точки пересечения прямых a и b, а также прямых b и c. Обозначим их как точки A и B соответственно. Эти точки являются вершинами углов, внутри которых будут строиться биссектрисы.
2. Рассматриваем угол, образованный прямыми a и b в точке A. Для построения биссектрисы этого угла из точки A проводим дугу произвольного радиуса, которая пересекает обе стороны угла. Обозначаем точки пересечения дуги со сторонами угла как P и Q. Затем из точек P и Q проводим дуги одинакового радиуса, которые пересекаются в некоторой точке внутри угла. Соединяем вершину угла A с точкой пересечения дуг. Полученная линия является биссектрисой угла при пересечении прямых a и b.
3. Повторяем аналогичную процедуру для угла, образованного прямыми b и c в точке B. Строим биссектрису этого угла, используя тот же метод.
4. Теперь у нас есть две биссектрисы: одна проходит через точку A для угла между прямыми a и b, другая проходит через точку B для угла между прямыми b и c.
5. Находим точки пересечения этих биссектрис. Первая биссектриса пересекает вторую в двух местах: в точках M1 и M2. Эти точки являются потенциальными решениями задачи.
6. Повторяем процедуру для других углов, образованных прямыми a, b и c. Строим биссектрисы для оставшихся углов и определяем их точки пересечения. В результате получаем еще две точки: M3 и M4.
7. Проверяем каждую из точек M1, M2, M3 и M4 на равноудаленность от прямых a, b и c. Для этого измеряем перпендикулярные расстояния от каждой из точек до всех трех прямых. Если расстояния равны, точка удовлетворяет условию задачи.
8. В результате получаем четыре точки: M1, M2, M3 и M4. Каждая из них равноудалена от прямых a, b и c.
Ответ: задача имеет четыре решения, которые представлены точками M1, M2, M3 и M4.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.