ГДЗ по Геометрии 7 класс Номер 357 Атанасян — Подробные Ответы

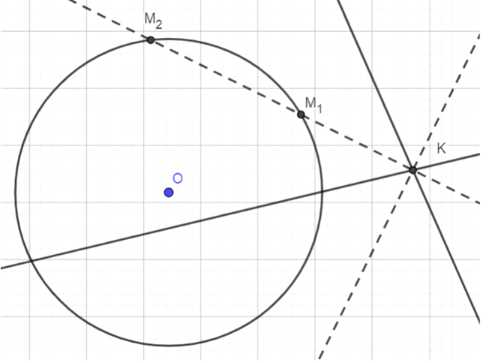
На данной окружности постройте точку, равноудалённую от двух данных пересекающихся прямых. Сколько решений может иметь задача?

Построим пересекающиеся прямые, образующие четыре угла.

Определим углы, внутри которых находится окружность. Построим биссектрисы этих углов. Удлиним биссектрисы до пересечения с окружностью. Отметим точки пересечения как искомые. Задача может иметь от 0 до 4 решений в зависимости от количества пересечений биссектрис с окружностью.

1. Построим две пересекающиеся прямые. Они образуют четыре угла. Определим, в каких из этих углов находится окружность.

2. Для каждого угла, внутри которого находится окружность, построим биссектрису. Для построения биссектрисы:
— Из вершины угла проведем дугу произвольного радиуса, которая пересечет обе стороны угла.
— Отметим точки пересечения дуги со сторонами угла.
— Проведем еще одну дугу из каждой из этих точек с одинаковым радиусом, чтобы они пересеклись внутри угла.
— Соединим вершину угла с точкой пересечения дуг. Полученная линия является биссектрисой.

3. Проведем биссектрисы всех углов, внутри которых находится окружность.

4. Найдем точки пересечения биссектрис с окружностью. Для этого:
— Удлиним каждую биссектрису до тех пор, пока она не пересечет окружность.
— Отметим точки пересечения биссектрис с окружностью.

5. Обозначим точки пересечения биссектрис с окружностью как M1, M2, M3 и M4.

6. Проверим, что каждая из отмеченных точек равноудалена от прямых. Точки M1, M2, M3 и M4 являются искомыми, так как они лежат на окружности и равноудалены от данных прямых.

Задача может иметь от 0 до 4 решений в зависимости от того, сколько раз биссектрисы пересекают окружность.