ГДЗ по Геометрии 7 класс Номер 356 Атанасян — Подробные Ответы

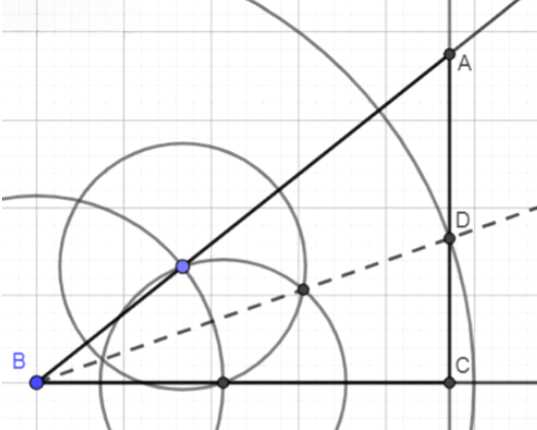
Постройте прямоугольный треугольник ABC, если даны острый угол В и биссектриса BD.

1. Построить угол B с лучами BX и BY.
2. Провести биссектрису угла B и отметить на ней точку D.
3. Из точки D провести перпендикуляр к лучу BY.
4. Перпендикуляр пересечет лучи BX и BY в точках A и C соответственно.
5. Соединить точки A, B и C. Полученный треугольник ABC будет прямоугольным.

1. Построим угол B произвольной величины. Обозначим его стороны лучами BX и BY.

2. Проведем биссектрису угла B. Для этого:
— Отметим на сторонах угла B две точки, одинаково удаленные от вершины B.
— Построим окружности с центрами в этих точках и равными радиусами.
— Точка пересечения окружностей внутри угла будет лежать на биссектрисе. Соединим эту точку с вершиной B. Полученная прямая — это биссектриса угла B.

3. На биссектрисе угла B отложим отрезок BD произвольной длины. Точка D лежит на биссектрисе.

4. Из точки D проведем прямую, перпендикулярную одной из сторон угла B (например, BY). Для этого:
— Через точку D проведем окружность произвольного радиуса, которая пересекает луч BY в двух точках.
— Построим серединный перпендикуляр к отрезку, соединяющему эти две точки. Этот перпендикуляр будет проходить через точку D.

5. Перпендикуляр, проведенный через точку D, пересечет стороны угла B в двух точках:
— В точке A — на стороне BX.
— В точке C — на стороне BY.

6. Соединим точки A, B и C. Получим треугольник ABC.

7. Проверим, что треугольник ABC прямоугольный:
— Угол B является прямым, так как по построению перпендикуляр из точки D делит угол B на две равные части.

Таким образом, треугольник ABC построен, и он является прямоугольным.