ГДЗ по Геометрии 7 класс Номер 355 Атанасян — Подробные Ответы

Точки A и B лежат по одну сторону от прямой а. Постройте точку М прямой а так, чтобы сумма AM + MB имела наименьшее значение, т. е. была бы меньше суммы АХ + ХВ, где X — любая точка прямой а, отличная от М.

Проведите из точки A перпендикуляр к прямой a и обозначьте точку пересечения как H.

Отложите на прямой a отрезок HA’ равный HA и обозначьте симметричную точку как A’. Соедините точки A’ и B, найдите точку пересечения отрезка A’B с прямой a и обозначьте ее как M. Точка M равноудалена от A и A

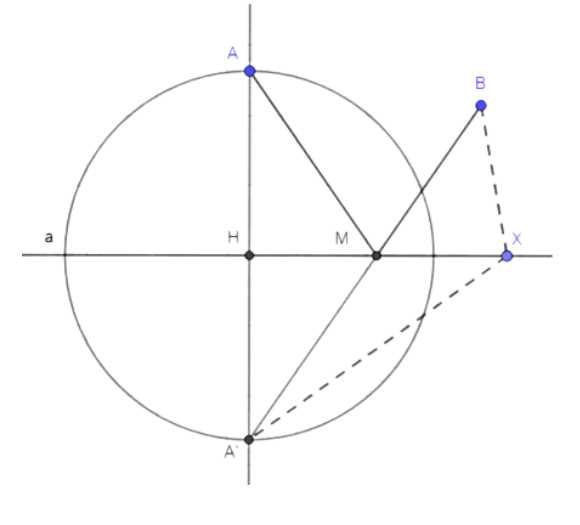
Построение точки M, принадлежащей прямой a, такой, что AM + MB < AX + XB, где X — произвольная точка, отличная от M:

1. Проведем перпендикуляр из точки A к прямой a. Для этого из точки A опускаем прямую, перпендикулярную a. Точку пересечения этой прямой с прямой a обозначим как H.

2. На прямой a отложим отрезок HA’ равный HA. Для этого измеряем длину отрезка HA и откладываем ее в противоположную сторону от точки H на прямой a. Точку, полученную в результате, обозначим как A’.

3. Соединим точки A’ и B прямой линией. Найдем точку пересечения отрезка A’B с прямой a. Эту точку обозначим как M.

4. Поскольку точка M равноудалена от A и A’, выполняется равенство AM = A’M. Таким образом, отрезок A’B равен сумме отрезков AM и MB.

5. Выберем произвольную точку X, отличную от M, на плоскости. Рассмотрим треугольник A’XB. В этом треугольнике по неравенству треугольника выполняется условие A’B < BX + A’X.

6. Из пункта 4 следует, что A’B = AM + MB. Следовательно, AM + MB < AX + XB, так как A’B меньше суммы отрезков BX и A’X.

Таким образом, точка M построена, и для любой точки X, отличной от M, выполняется условие AM + MB < AX + XB.